
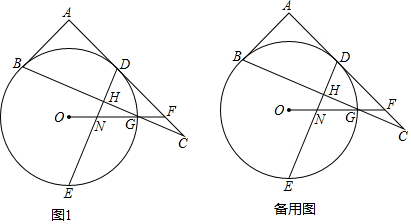
分析 (1)先判断出四边形ABOD是正方形,用圆的性质得出∠OBG=∠OGB=22.5°,进而求出∠C=22.5°,∠DNF=67.5°,即可得出结论;
(2)借助(1)的结论先判断出FN=FD,再判断出FD=OG,最后代换即可得出结论;
(3)先判断出BD=CD,用面积求出圆的半径,即可求出四边形ABED的面积.
解答 解:(1)如图1,
∵∠BAC=90°,
∴∠C+∠ABC=90°,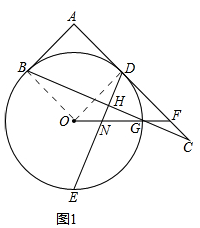 连接OB,OD,
连接OB,OD,
∵⊙O分别与AB、AC相切于点B、点D,
∴∠ABO=∠ADO=90°,
∴∠OBC+∠ABC=90°,
∴∠OBC=∠C,
∵∠ODC=90°,∠AFO=45°,
∴∠DOF=45°
∵∠BAD=90°,
∴四边形ABOD是矩形,
∴∠BOD=90°,
∴∠BOG=∠BOD+∠DOF=135°,
∵OB=OG,
∴∠OBG=∠OGB=22.5°,
∴∠C=∠OBC=22.5°,
在四边形ABHD中,
∵DH⊥BC,
∴∠BHD=90°,
∵∠A=90°,
∴∠ABH+∠ADH=180°,
∴∠ABO-∠OBC+∠ADO+∠ODN=180°,
∵∠ABO=∠ADO=90°,
∴∠ODN=∠OBC=22.5°,
∴∠DNF=∠DOF+∠ODN=45°+22.5°=67.5°,
∵∠C=22.5°,
∴∠FDN=3∠C,
(2)如图2,
由(1)知,∠ODN=22.5°,
∴∠FDN=67.5°=∠DNF,
∴FN=FD,
在Rt△ODF中,∠AFO=45°,
∴FD=OD=OG=ON+NG,
∵FN=ON+NG,
∴FG=ON,
∵∠BOF=135°,
∴∠MON=45°,
∵∠ONM=∠DNF=67.5°,
∴∠OMN=67.5°,
∴OM=ON,
∴OM=FG,
(3)如图3,设⊙O的半径为R,
∴AB=AD=OB=R,
∴BD=$\sqrt{2}$OB=$\sqrt{2}$R,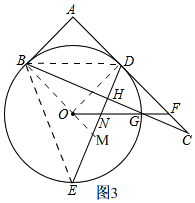 由(2)知,∠CDH=67.5°,
由(2)知,∠CDH=67.5°,
由(1)知,∠ODN=22.5°,
∵∠ODB=45°,
∴∠BDH=67.5°,
∴∠BDH=∠CDH,
∵DH⊥BC,
∴CD=BD=$\sqrt{2}$R,
∴AC=AD+CD=($\sqrt{2}$+1)R,
∵BD是正方形ABOD的对角线,
∴S△ABD=S△OBD
∵由BC、DC和弧BD所围成图形的面积为$\frac{9}{4}$π+$\frac{9}{2}$$\sqrt{2}$-$\frac{9}{2}$,
∴$\frac{9}{4}$π+$\frac{9}{2}$$\sqrt{2}$-$\frac{9}{2}$=S△ABC-S△ABD+S弓形BD
=S△ABC-S△ABD+S扇形OBD-S△BDO=S△ABC+S扇形OBD-2S△BDO=$\frac{1}{2}$AB×AC+$\frac{90°π{R}^{2}}{360°}$-2×$\frac{1}{2}$OB2=$\frac{1}{2}$R×($\sqrt{2}$+1)R+$\frac{π{R}^{2}}{4}$-R2=($\frac{π}{4}$-$\frac{1}{2}$+$\frac{\sqrt{2}}{2}$)R2,
∴R=3,
∵∠BDE=67.5°,∠E=$\frac{1}{2}$∠BOD=45°,
∴∠EBD=67.5°=∠BDE,
∴BE=DE,
∵OB=OD,
∴点O,E都在BD的垂直平分线上,
∴△BDE的边BD上的高h=R+$\frac{\sqrt{2}}{2}$,
∴S四边形ABED=S△ABD+S△BDE=$\frac{1}{2}$×$\sqrt{2}R×\frac{\sqrt{2}}{2}R$+$\frac{1}{2}×\sqrt{2}R×(R+\frac{\sqrt{2}}{2}R)$=(1+$\frac{\sqrt{2}}{2}$)R2=9+$\frac{9\sqrt{2}}{2}$.
点评 此题是圆的综合题,主要考查了圆的性质,正方形的判定,直角三角形的性质,三角形的面积,扇形的面积,解本题的关键是得出∠C=22.5°和判断出DB=DC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
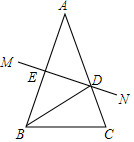 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
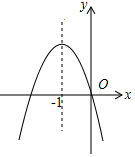 已知二次函数y=ax2+bx+c(a≠0)的图象如图,以下结论正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,以下结论正确的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
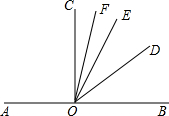 在直线AB上取一点O,在AB同侧引射线OC,OD,OE,OF,使∠BOE与∠COE互余,射线OF和OD分别平分∠COE和∠BOE,试说明∠AOF+∠BOD=3∠DOF.
在直线AB上取一点O,在AB同侧引射线OC,OD,OE,OF,使∠BOE与∠COE互余,射线OF和OD分别平分∠COE和∠BOE,试说明∠AOF+∠BOD=3∠DOF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com