
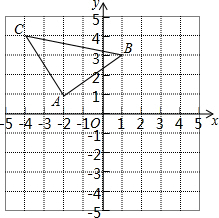
 如图,方格纸中每个小正方形的边长都是1个单位长度,建立平面直角坐标系后,△ABC的顶点均在格点上,点A的坐标为(-2,1).
如图,方格纸中每个小正方形的边长都是1个单位长度,建立平面直角坐标系后,△ABC的顶点均在格点上,点A的坐标为(-2,1).分析 (1)利用关于y轴对称的性质得出A,B,C对应点坐标,进而得出答案;
(2)利用旋转的性质分别得出对应点位置,进而得出图形,再利用扇形面积求法得出即可.
解答  解:(1)如图所示:△A1B1C1即为所求,点A1的坐标为:(2,1);
解:(1)如图所示:△A1B1C1即为所求,点A1的坐标为:(2,1);
(2)如图所示:△A2B2C2即为所求,
线段B1C1在旋转过程中所扫过的面积为:
S=S△OC1B1+S扇形C1OC2-S扇形B1OB2-S△OC2B2
=S扇形C1OC2-S扇形BOB2
=$\frac{90π×(4\sqrt{2})^{2}}{360}$-$\frac{90π×(\sqrt{10})^{2}}{360}$
=$\frac{11}{2}$π.
点评 此题主要考查了扇形面积公式的应用以及图象的平移和旋转,根据已知得出对应点位置是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当AB=BC时,?ABCD是菱形 | B. | 当∠ABC=90°时,?ABCD是矩形 | ||
| C. | 当AC⊥BD时,?ABCD是菱形 | D. | 当AC=BD时,?ABCD是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
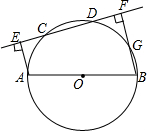 如图所示,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD交直线CD于点E,BF⊥CD交直线CD于点F,若BF交⊙O于G.求证:$\widehat{AC}$=$\widehat{DG}$.
如图所示,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD交直线CD于点E,BF⊥CD交直线CD于点F,若BF交⊙O于G.求证:$\widehat{AC}$=$\widehat{DG}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com