
【题目】(2017·河北迁安一模)如图,在Rt△ABC中,直角边AC=7 cm,BC=3 cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2 cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
(1)试说明:∠A=∠BCD;
(2)点E运动多长时间,CF=AB?并说明理由.


【答案】(1)理由见解析;(2)当点E在射线BC上移动5 s或2 s时,CF=AB.
【解析】试题分析:(1)、根据同角的余角相等得出答案;(2)、首先根据题意画出两个不同的图形,然后根据三角形全等得出线段的长度,从而得出运动的时间.
试题解析:(1)因为∠A+∠ACD=90°,∠BCD+∠ACD=90°, 所以∠A=∠BCD.
(2)如图,当点E在射线BC上移动时,若点E移动5 s,则BE=2×5=10(cm),
所以CE=BE-BC=10-3=7(cm). 所以CE=AC.
在△CFE与△ABC中,  所以△CFE≌△ABC, 所以CF=AB.
所以△CFE≌△ABC, 所以CF=AB.
当点E在射线CB上移动时,若点E移动2 s,则BE'=2×2=4(cm),
所以CE'=BE'+BC=4+3=7(cm), 所以CE'=AC.
在△CF'E'与△ABC中,  所以△CF'E'≌△ABC. 所以CF'=AB.
所以△CF'E'≌△ABC. 所以CF'=AB.
总之,当点E在射线BC上移动5 s或2 s时,CF=AB.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】坐标平面上,某二次函数图形的顶点为(2,﹣1),此函数图形与x轴相交于P、Q两点,且PQ=6.若此函数图形通过(1,a)、(3,b)、(﹣1,c)、(﹣3,d)四点,则a、b、c、d之值何者为正?( )
A.a
B.b
C.c
D.d
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在城中村改造中,需要种植![]() 、
、![]() 两种不同的树苗共
两种不同的树苗共![]() 棵,经招标,承包商以
棵,经招标,承包商以![]() 万元的报价中标承包了这项工程,根据调查及相关资料表明,
万元的报价中标承包了这项工程,根据调查及相关资料表明, ![]() 、
、![]() 两种树苗的成本价及成活率如表:
两种树苗的成本价及成活率如表:
品种 | 购买价(元/棵) | 成活率 |
|
|
|
|
|
|
设种植![]() 种树苗
种树苗![]() 棵,承包商获得的利润为
棵,承包商获得的利润为![]() 元.
元.
(![]() )求
)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(![]() )政府要求栽植这批树苗的成活率不低于
)政府要求栽植这批树苗的成活率不低于![]() ,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
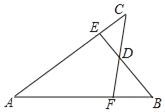
A. ① B. ② C. ①和② D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子有:①90°﹣∠β;②∠α﹣90°;③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠α﹣∠β),其中错误的有( )个
(∠α﹣∠β),其中错误的有( )个
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△APE中,∠PAE=90°,PO是△APE的角平分线,以O为圆心,OA为半径作圆交AE于点G.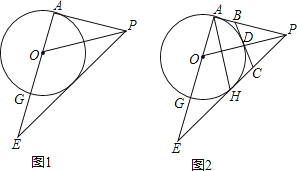
(1)求证:直线PE是⊙O的切线;
(2)在图2中,设PE与⊙O相切于点H,连结AH,点D是⊙O的劣弧 ![]() 上一点,过点D作⊙O的切线,交PA于点B,交PE于点C,已知△PBC的周长为4,tan∠EAH=
上一点,过点D作⊙O的切线,交PA于点B,交PE于点C,已知△PBC的周长为4,tan∠EAH= ![]() ,求EH的长.
,求EH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形中,两条直角边的长度分别为a和b,斜边长度为c,则a2+b2=c2,即两条直角边的平方和等于斜边的平方,此结论称为勾股定理.在一张纸上画两个同样大小的直角三角形ABC和A′B′C′,并把它们拼成如图所示的形状 (点C和A′重合,且两直角三角形的斜边互相垂直).请利用拼得的图形证明勾股定理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三个角是∠A,∠B,∠C ,它们所对的边分别是a,b,c.①c2-a2=b2;②∠A=![]() ∠B=
∠B=![]() ∠C;③c=
∠C;③c=![]() a=
a=![]() b;④a=2,b=2
b;④a=2,b=2 ![]() ,c=
,c=![]() .上述四个条件中,能判定△ABC 为直角三角形的有( )
.上述四个条件中,能判定△ABC 为直角三角形的有( )
A. 1个 B. 2个
C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com