
 如图,矩形ABCD(AD>AB),AB=1,问BC边上是否存在点M,使得AM⊥DM.
如图,矩形ABCD(AD>AB),AB=1,问BC边上是否存在点M,使得AM⊥DM. 分析 如图,当AD=2,点M是BC中点时,△AMD是直角三角形,由此即可判定.
解答 解:如图,当AD=2,点M是BC中点时,△AMD是直角三角形,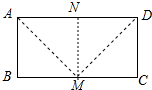
理由:取AD中点N,连接MN.
∵四边形ABCD是矩形,
∴BC=AD,AD∥BC,∠BAD=90°,
∵AN∥BM,AN=BM,
∴四边形ABMN是平行四边形,
∴MN=AB=1,
∵AN=ND=1,
∴MN=NA=ND,
∴△AMD是直角三角形.
由此可知,当AD≥2时,BC边上是否存在点M,使得AM⊥DM,
当AD<2时,BC边上不存在点M,使得AM⊥DM,
点评 本题考查矩形的性质、直角三角形的判定等知识,解题的关键是判断出AD=2时存在Rt△ADM,题目比较抽象,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
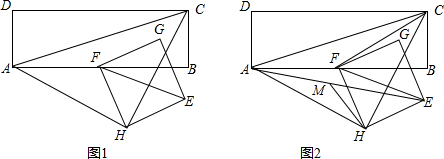
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
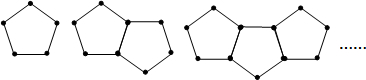
| A. | 33 | B. | 32 | C. | 31 | D. | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为36m,机场平行于墙的一边长y(m)与垂直于墙的一边a(m)的函数关系式是y=-2a+36;自变量a的取值范围是9≤a≤18.
如图,在靠墙(墙长为18m)的地方围建一个矩形的养鸡场,另三边用竹篱笆围成,如果竹篱笆总长为36m,机场平行于墙的一边长y(m)与垂直于墙的一边a(m)的函数关系式是y=-2a+36;自变量a的取值范围是9≤a≤18.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上,若BC=80,AD=60,PN=2PQ,求矩形PQMN的面积.
如图,在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上,若BC=80,AD=60,PN=2PQ,求矩形PQMN的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com