
 如图是一个育苗棚,棚宽a=12m,棚高b=5m,棚长d=10m,则覆盖在棚斜面上的塑料薄膜的面积为130m2.
如图是一个育苗棚,棚宽a=12m,棚高b=5m,棚长d=10m,则覆盖在棚斜面上的塑料薄膜的面积为130m2.  英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
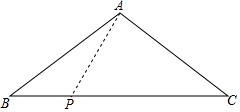
 如图,点P在△ABC的边AC上,添加一个条件可判断△ABP∽△ACB,其中添加不正确的是( )
如图,点P在△ABC的边AC上,添加一个条件可判断△ABP∽△ACB,其中添加不正确的是( )| A. | ∠ABP=∠C | B. | ∠APB=∠ABC | C. | $\frac{AP}{AB}$=$\frac{AB}{AC}$ | D. | $\frac{AB}{AP}$=$\frac{CB}{BP}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
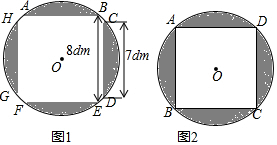
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等腰三角形ABC的底边长为8cm,腰长为5cm,一动点P在底边上从点B向点C以1cm/s的速度移动,
如图,等腰三角形ABC的底边长为8cm,腰长为5cm,一动点P在底边上从点B向点C以1cm/s的速度移动,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com