
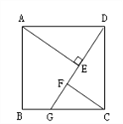
【题目】四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF∥AE交DG于F.
(1) 在图中找出一对全等三角形,并加以证明;
(2)求证:AE=FC+EF.
科目:初中数学 来源: 题型:
【题目】如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.求E应建在距A多远处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】回答下列问题:
(1)计算:①(x+2)(x+3)= ;② (x +7)( x-10)= ;③(x-5)(x-6)= .
(2)总结公式:(x+a)(x+b)= .
(3)已知a,b,m均为整数,且(x+a)(x+b)=x2+mx+6,求m的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 如果![]() ,则
,则 ![]()
B. 如果|a|=|b|,那么a=b
C. 两个锐角的和是钝角
D. 如果一点到线段两端的距离相等,那么这点是这条线段的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把带有指针的圆形转盘A、B分别分成4等份、3等份的扇形区域,并在每一个小区域内标上数字(如图所示).小明、小乐两个人玩转盘游戏,游戏规则是:同时转动两个转盘,当转盘停止时,若指针所指两区域的数字之积为3的倍数,则小明胜;否则,小乐胜.(若有指针落在分割线上,则无效,需重新转动转盘) 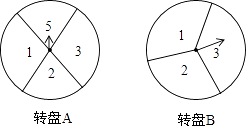
(1)试用列表或画树状图的方法,求小明获胜的概率;
(2)请问这个游戏规则对小明、小乐双方公平吗?做出判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数![]() 的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
(1)求一次函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出y1>y2时x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com