
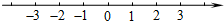 (1)计算:(3-π)0+2tan60°+(-1)2015-$\sqrt{12}$.
(1)计算:(3-π)0+2tan60°+(-1)2015-$\sqrt{12}$.分析 (1)根据零指数幂、特殊角的三角函数值以及二次根式的化简的知识求解即可求得答案;
(2)首先分别求得各不等式的解集,继而求得不等式组的解集.
解答 解:(1)计算:(3-π)0+2tan60°+(-1)2015-$\sqrt{12}$.
=1+2$\sqrt{3}$-1-2$\sqrt{3}$
=0;
(2)$\left\{\begin{array}{l}{x+3>1①}\\{x+2(x-1)≤1②}\end{array}\right.$,
由①得:x>-2,
由②得:x≤1,
∴原不等式的解集为:-2<x≤1.
在数轴上表示为:
点评 此题考查了零指数幂、二次根式的化简、特殊角的三角函数值以及不等式组的解法.注意用数轴表示不等式的解集时,要注意“两定”:一是定界点,一般在数轴上只标出原点和界点即可.定边界点时要注意,点是实心还是空心,若边界点含于解集为实心点,不含于解集即为空心点;二是定方向,定方向的原则是:“小于向左,大于向右”.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com