
【题目】如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE,连接DE并延长交射线AP于点F,连接BF
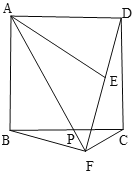
(1)若![]() ,直接写出
,直接写出![]() 的大小(用含
的大小(用含![]() 的式子表示).
的式子表示).
(2)求证:![]() .
.
(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.
【答案】(1)45°+![]() ;(2)证明见解析;(3)AF=
;(2)证明见解析;(3)AF=![]() BF+CF.
BF+CF.
【解析】
(1)过点A作AG⊥DF于G,由轴对称性质和正方形的性质可得AE=AD,∠BAP=∠EAF,根据等腰三角形“三线合一”的性质可得∠EAG=∠DAG,即可得∠FAG=![]() ∠BAD=45°,∠DAG+∠BAP=45°,根据直角三角形两锐角互余的性质即可得答案;
∠BAD=45°,∠DAG+∠BAP=45°,根据直角三角形两锐角互余的性质即可得答案;
(2)由(1)可得∠FAG=![]() ∠BAD=45°,由AG⊥PD可得∠APG=45°,根据轴对称的性质可得∠BPA=∠APG=45°,可得∠BFD=90°,即可证明BF⊥DF;
∠BAD=45°,由AG⊥PD可得∠APG=45°,根据轴对称的性质可得∠BPA=∠APG=45°,可得∠BFD=90°,即可证明BF⊥DF;
(3)连接BD、BE,过点C作CH//FD,交BE延长线于H,由∠BFD=∠BCD=90°可得B、F、C、D四点共圆,根据圆周角定理可得∠FBC=∠FDC,∠DFC=∠DBC=45°,根据平行线的性质可得∠FDC=∠DCH,根据角的和差关系可得∠ABF=∠BCH,由轴对称性质可得BF=EF,可得△BEF是等腰直角三角形,即可得∠BEF=45°,BE=![]() BF,即可证明∠BEF=∠DFC,可得BH//FC,即可证明四边形EFCH是平行四边形,可得EH=FC,EF=CH,利用等量代换可得CH=BF,利用SAS可证明△ABF≌△BCH,可得AF=BH,即可得AF、BF、CF的数量关系.
BF,即可证明∠BEF=∠DFC,可得BH//FC,即可证明四边形EFCH是平行四边形,可得EH=FC,EF=CH,利用等量代换可得CH=BF,利用SAS可证明△ABF≌△BCH,可得AF=BH,即可得AF、BF、CF的数量关系.
(1)过点A作AG⊥DF于G,
∵点B关于直线AF的对称点为E,四边形ABCD是正方形,
∴AE=AB,AB=AD=DC=BC,∠BAF=∠EAF,
∴AE=AD,
∵AG⊥FD,
∴∠EAG=∠DAG,
∴∠BAF+∠DAG=∠EAF+∠EAG,
∵∠BAF+∠DAG+∠EAF+∠EAG=∠BAD=90°,
∴∠BAF+∠DAG=∠GAF=45°,
∴∠DAG=45°-![]() ,
,
∴∠ADF=90°-∠DAG=45°+![]() .
.
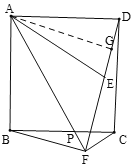
(2)由(1)得∠GAF=45°,
∵AG⊥FD,
∴∠AFG=45°,
∵点E、B关于直线AF对称,
∴∠AFB=∠AFE=45°,
∴∠BFG=90°,
∴BF⊥DF.
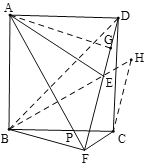
(3)连接BD、BE,过点C作CH//FD,交BE延长线于H,
∵∠BFD=∠BCD=90°,
∴B、F、C、D四点共圆,
∴∠FDC=∠FBC,∠DFC=∠DBC=45°,
∵CH//FD,
∴∠DCH=∠FDC,
∴∠FBC=∠DCH,
∵∠ABC=∠BCD=90°,
∴∠ABC+∠FBC=∠BCD+∠DCH,即∠ABF=∠BCH,
∵点E、B关于直线AF对称,
∴BF=EF,
∵∠BFE=90°,
∴△BEF是等腰直角三角形,
∴∠BEF=45°,BE=![]() BF,
BF,
∴∠BEF=∠DFC,
∴FC//BH,
∴四边形EFCH是平行四边形,
∴EH=FC,CH=BF,
在△ABF和△BCH中,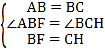 ,
,
∴AF=BH=BE+EH=![]() BF+CF.
BF+CF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
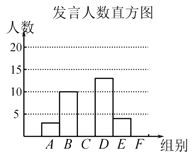
【题目】2020年春节前夕“新型冠状病毒”爆发,国家教育部要求各地延期开学,并要求:利用网络平台,“停课不停学”.为响应号召,某校师生根据上级要求积极开展网络授课教学,八年级为了解学生网课发言情况,随机抽取该年级部分学生,对他们某天在网课上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)求出样本容量,并补全直方图,在扇形统计图中,“B”所对应的圆心角的度数是 ;
(2)该年级共有学生500人,估计全年级在这天里发言次数不少于12的人数为 ;
(3)该校八年级组织一次网络授课经验专项视频会议,A组的中恰有1位女生,E组的中有位2男生.现从A组与E组中分别抽一位写报告,利用“树状图”或列表法求出正好选中一男一女的概率.
n | |
A |
|
B |
|
C |
|
D |
|
E |
|
F |
|

查看答案和解析>>
科目:初中数学 来源: 题型:
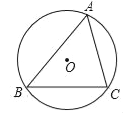
【题目】如图,△ABC内接于⊙O.
(1)作∠B的平分线与⊙O交于点D(用尺规作图,不用写作法,但要保留作图痕迹);
(2)在(1)中,连接AD,若∠BAC=60°,∠C=66°,求∠DAC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
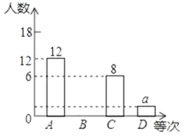
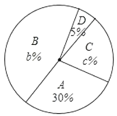
【题目】2020年,一场突然而来的新型冠状病毒肺炎疫情阻挡了学生们开学的脚步,多地学校进行了“战役在家,线上课堂”活动,保证学生离校不离学,为减少初中生被网络诈骗的案件,因此要求学生掌握防诈骗知识并进行网络测评.为了解某校学生的测试情况,从中随机抽取部分学生的成绩进行统计,并把测试成绩分为A.B.C.D四个等次,绘制成如图所示的不完整的统计图,请你依图解答下列问题:
(1)a= ,b= ,c= ;
(2)请将条形统计图补充完整,并计算表示C等次的扇形所对的圆心角的度数;
(3)学校决定从A等次的甲、乙、丙、丁四名学生中,随机选取两名学生参加全市中学生防网络诈骗知识竞赛,请用列表法或画树状图法,求甲、乙两名学生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC⊥AB,O为AC的中点,经过点O的直线交AD于E,交BC于F,连结AF、CE,现在添加一个适当的条件,使四边形AFCE是菱形,下列条件:①OE=OA;②EF⊥AC;③AF平分∠BAC;④E为AD中点.正确的有( )个.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A是y轴上一点,其坐标为(0,6),点B在x轴的正半轴上.点P,Q均在线段AB上,点P的横坐标为m,点Q的横坐标大于m,在△PQM中,若PM∥x轴,QM∥y轴,则称△PQM为点P,Q的“肩三角形.
(1)若点B坐标为(4,0),且m=2,则点P,B的“肩三角形”的面积为 ;
(2)当点P,Q的“肩三角形”是等腰三角形时,求点B的坐标;
(3)在(2)的条件下,作过O,P,B三点的抛物线y=ax2+bx+c
①若M点必为抛物线上一点,求点P,Q的“肩三角形”面积S与m之间的函数关系式,并写出自变量m的取值范围.
②当点P,Q的“肩三角形”面积为3,且抛物线y=ax2+bx+c与点P,Q的“肩三角形”恰有两个交点时,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com