
”¾ĢāÄæ”æŅŃÖŖÅ×ĪļĻßy£½ax2+bx+cÓėxÖį½»ÓŚO”¢BĮ½µć£¬Ę䶄µćA×ų±źĪŖ£Ø1£¬1£©£¬µćCĪŖÅ×ĪļĻßŌŚµŚĖÄĻóĻŽÄŚµÄŅ»µć£¬Ęä×ų±źĪŖ£Ø3£¬©3£©£®
£Ø1£©ĒóÅ×ĪļĻß½āĪöŹ½£»
£Ø2£©µćDĪŖÅ×ĪļĻßŌŚµŚČżĻóĻŽÄŚµÄŅ»µć£¬¹żµćDĻņxÖį×÷“¹Ļ߶Ī£¬“¹×ćĪŖH£¬ŹĒ·ń“ęŌŚµćDŹ¹µĆ”÷DHOÓė”÷AOCĻąĖĘ£¬Čē¹ū“ęŌŚ£¬ĒėĒó³öµćD×ų±ź£¬Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©µćE”¢F·Ö±šĪŖÅ×ĪļĻßŅŌ¼°Å×ĪļĻ߶Ō³ĘÖįÉĻµÄĮ½¶Æµć£¬ĒėĪŹŹĒ·ń“ęŌŚŅŌBOĪŖ±ß£¬B”¢O”¢E”¢FĪŖ¶„µćµÄĘ½ŠŠĖıߊĪ£¬Čē¹ū“ęŌŚĒėÖ±½ÓŠ“³öµćE×ų±ź£¬Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
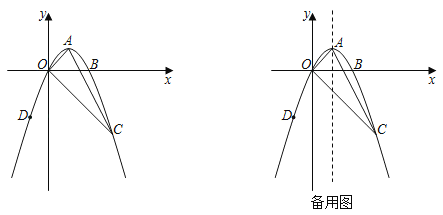
”¾“š°ø”æ£Ø1£©y£½©x2+2x£»£Ø2£©“ęŌŚ£¬D£Ø©1£¬©3£©£»£Ø3£©“ęŌŚ£¬µćEµÄ×ų±źĪŖ£Ø©1£¬©3£©»ņ£Ø3£¬©3£©£®
”¾½āĪö”æ
£Ø1£©ÓÉĢāŅāÉč³ö¶„µćŹ½½āĪöŹ½y£½a£Øx©1£©2+1£¬ŌŁ½«µćC“śČė¼“æÉ£»
£Ø2£©ÉčµćDµÄ×ų±źĪŖ£Øm£¬©m2+2m£©£¬×÷DH”ĶxÖį£¬“¹Ö±ĪŖH£¬Į¬½ÓOD£®·Ö±šĒó³öAO£½![]() £¬OC£½3
£¬OC£½3![]() £¬·ÖĮ½ÖÖĒéæö¢Ł
£¬·ÖĮ½ÖÖĒéæö¢Ł![]() £½
£½![]() £¬Ōņ
£¬Ōņ![]() £½
£½![]() £½
£½![]() £¬ÓÉHO£½©m£¬HD£½m2©2m£¬æɵĆ
£¬ÓÉHO£½©m£¬HD£½m2©2m£¬æɵĆ![]() £½
£½![]() £¬½āµĆ¼“æÉ£»¢Ś
£¬½āµĆ¼“æÉ£»¢Ś![]() £½
£½![]() £¬Ōņ
£¬Ōņ![]() £½
£½![]() £½
£½![]() £¬ÓÉHO£½©m£¬HD£½m2©2m£¬æɵĆ
£¬ÓÉHO£½©m£¬HD£½m2©2m£¬æɵĆ![]() £½
£½![]() £¬½āµĆ¼“æÉ£»
£¬½āµĆ¼“æÉ£»
£Ø3£©ÉčµćE£Øa£¬©a2+2a£©£¬ŌņF£Ø1£¬©a2+2a£©£¬¢Łµ±OEFBĪŖĘ½ŠŠĖıߊĪŹ±£¬OB£½EF£¬ĖłŅŌ1©a£½2£¬ŌņE£Ø©1£¬©3£©£»¢Śµ±OFEBĪŖĘ½ŠŠĖıߊĪŹ±£¬OB£½FE£¬ĖłŅŌa©1£½2£¬¼“æÉµĆ³öµćEµÄ×ų±ź£®
½ā£ŗ£Ø1£©ÓÉĢāŅāæÉÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖy£½a£Øx©1£©2+1£¬
”ßÅ×ĪļĻß¾¹żµćC£Ø3£¬©3£©£¬
”ą©3£½a£Ø3©1£©2+1£¬
”ąa£½©1£¬
”ąy£½©x2+2x£»
£Ø2£©ÉčµćDµÄ×ų±źĪŖ£Øm£¬©m2+2m£©£¬×÷DH”ĶxÖį£¬“¹Ö±ĪŖH£¬Į¬½ÓOD£®
”ßA£Ø1£¬1£©£¬C£Ø3£¬©3£©£¬
”ąµćA”¢C·Ö±šŌŚŅ»”¢ČżĻóĻŽ½ĒĘ½·ÖĻßÓė¶ž”¢ĖÄĻóĻŽ½ĒĘ½·ÖĻßÉĻ£¬
”ą”ĻAOC£½90”ć£¬
”ąAO£½![]() £¬OC£½3
£¬OC£½3![]() £¬
£¬
Čō”÷DHOÓė”÷AOCĻąĖĘ£¬
”ß”ĻDHO£½”ĻAOC£½90”ć£¬
¢Ł![]() £½
£½![]() £¬
£¬
”ą![]() £½
£½![]() £½
£½![]() £¬
£¬
”ßHO£½©m£¬HD£½m2©2m£¬
”ą![]() £½
£½![]() £¬
£¬
½āµĆm£½©1»ņm£½0£ØÉį£©£¬
”ąD£Ø©1£¬3£©£»
¢Ś![]() £½
£½![]() £¬
£¬
”ą![]() £½
£½![]() £½
£½![]() £¬
£¬
”ßHO£½©m£¬HD£½m2©2m£¬
”ą![]() £½
£½![]() £¬
£¬
½āµĆm£½![]() £ØÉį£©»ņm£½0£ØÉį£©£»
£ØÉį£©»ņm£½0£ØÉį£©£»
×ŪÉĻĖłŹö£ŗD£Ø©1£¬©3£©£»
£Ø3£©“ęŌŚ£¬µćEµÄ×ų±źĪŖ£Ø©1£¬©3£©»ņ£Ø3£¬©3£©£®
ĄķÓÉČēĻĀ£ŗŅŌBOĪŖ±ß£¬B”¢O”¢E”¢FĪŖ¶„µćµÄĘ½ŠŠĖıߊĪ£¬
”ąOB”ĪEFĒŅOB£½EF£½2£¬
ÉčµćE£Øa£¬©a2+2a£©£¬ŌņF£Ø1£¬©a2+2a£©£¬
¢Łµ±OEFBĪŖĘ½ŠŠĖıߊĪŹ±£¬OB£½EF£¬
”ą1©a£½2£¬
”ąa£½©1£¬
”ąE£Ø©1£¬©3£©£»
¢Śµ±OFEBĪŖĘ½ŠŠĖıߊĪŹ±£¬OB£½FE£¬
”ąa©1£½2£¬
”ąa£½3£¬
”ąE£Ø3£¬©3£©£»
×ŪÉĻĖłŹö£¬“ęŌŚŅŌBOĪŖ±ß£¬B”¢O”¢E”¢FĪŖ¶„µćµÄĘ½ŠŠĖıߊĪ£¬µćEµÄ×ų±źĪŖ£Ø©1£¬©3£©»ņ£Ø3£¬©3£©£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy1=-x+4ÓėĖ«ĒśĻßy=![]() £Øk”Ł0£©½»ÓŚA”¢BĮ½µć£¬µćAµÄ×ų±źĪŖ£Ø1£¬m£©£¬¾¹żµćAµÄÖ±Ļßy2=x+bÓėxÖį½»ÓŚµćC£®
£Øk”Ł0£©½»ÓŚA”¢BĮ½µć£¬µćAµÄ×ų±źĪŖ£Ø1£¬m£©£¬¾¹żµćAµÄÖ±Ļßy2=x+bÓėxÖį½»ÓŚµćC£®
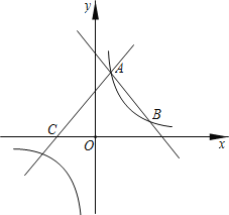
£Ø1£©Ē󷓱ȥżŗÆŹżµÄ±ķ“ļŹ½ŅŌ¼°µćCµÄ×ų±ź£»
£Ø2£©µćPŹĒxÖįÉĻŅ»¶Æµć£¬Į¬½ÓAP£¬Čō”÷ACPŹĒ”÷AOBµÄĆ껿µÄŅ»°ė£¬Ēó“ĖŹ±µćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹż![]() ÖŠµÄ
ÖŠµÄ![]() £¬
£¬![]() Āś×ćĻĀ±ķ
Āś×ćĻĀ±ķ
| ” |
| 0 | 1 | 2 | 3 | ” |
| ” | 0 |
|
|
|
| ” |
£Øl£©![]() ________£¬
________£¬![]() ________£»
________£»
£Ø2£©ŗÆŹżĶ¼Ļó¶Ō³ĘÖįŹĒ____________£»
£Ø3£©Čē¹ūµć![]() £¬
£¬![]() ŹĒĶ¼ĻóÉĻµć£¬Ōņ
ŹĒĶ¼ĻóÉĻµć£¬Ōņ![]() ________£»
________£»
£Ø4£©ŗÆŹżĶ¼ĻóÓė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() ”¢µć
”¢µć![]() £¬
£¬![]() ŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
ŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬![]() £¬Ōņµć
£¬Ōņµć![]() ×ų±źĪŖ________£®
×ų±źĪŖ________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
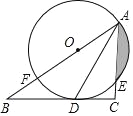
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬![]() £¬ADĘ½·Ö”ĻBAC£¬½»BCÓŚµćD£¬µćOŌŚABÉĻ£¬”ŃO¾¹żA”¢DĮ½µć£¬½»ACÓŚµćE£¬½»ABÓŚµćF£®
£¬ADĘ½·Ö”ĻBAC£¬½»BCÓŚµćD£¬µćOŌŚABÉĻ£¬”ŃO¾¹żA”¢DĮ½µć£¬½»ACÓŚµćE£¬½»ABÓŚµćF£®
£Ø1£©ĒóÖ¤£ŗBCŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©Čō”ŃOµÄ°ė¾¶ŹĒ2cm£¬EŹĒ»”ADµÄÖŠµć£¬ĒóŅõÓ°²æ·ÖµÄĆ껿£Ø½į¹ū±£Įō¦ŠŗĶøłŗÅ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
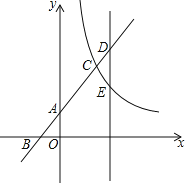
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬Ö±Ļßy£½x+2Óė×ų±źÖį½»ÓŚA”¢BĮ½µć£¬Óė·“±ČĄżŗÆŹży£½![]() £Øx£¾0£©½»ÓŚµćC£¬ŅŃÖŖAC£½2AB£®
£Øx£¾0£©½»ÓŚµćC£¬ŅŃÖŖAC£½2AB£®
£Ø1£©Ē󷓱ȥżŗÆŹż½āĪöŹ½£»
£Ø2£©ČōŌŚµćCµÄÓŅ²ąÓŠŅ»Ę½ŠŠÓŚyÖįµÄÖ±Ļߣ¬·Ö±š½»Ņ»“ĪŗÆŹżĶ¼ĻóÓė·“±ČĄżŗÆŹżĶ¼ĻóÓŚD”¢EĮ½µć£¬ČōCD£½CE£¬ĒóµćD×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
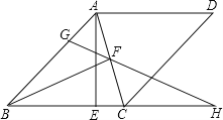
”¾ĢāÄæ”æ ĮāŠĪABCDÖŠ£¬FŹĒ¶Ō½ĒĻßACµÄÖŠµć£¬¹żµćA×÷AE”ĶBC“¹×ćĪŖE£¬GĪŖĻ߶ĪABÉĻŅ»µć£¬Į¬½ÓGF²¢ŃÓ³¤½»Ö±ĻßBCÓŚµćH£®
£Ø1£©µ±”ĻCAE=30”揱£¬ĒŅCE=![]() £¬ĒóĮāŠĪµÄĆ껿£»
£¬ĒóĮāŠĪµÄĆ껿£»
£Ø2£©µ±”ĻBGF+”ĻBCF=180”ć£¬AE=BEŹ±£¬ĒóÖ¤£ŗBF=(![]() +1)GF£®
+1)GF£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬½«Į½æéČ«µČµÄÖ±½ĒČż½ĒŠĪÖ½Ę¬”÷ABCŗĶ”÷DEFµž·ÅŌŚŅ»Ęš£¬ĘäÖŠ”ĻACB£½”ĻE£½90”ć£¬BC£½DE£½6£¬AC£½FE£½8£¬¶„µćDÓė±ßABµÄÖŠµćÖŲŗĻ£®
£Ø1£©ČōDE¾¹żµćC£¬DF½»ACÓŚµćG£¬ĒóÖŲµž²æ·Ö£Ø”÷DCG£©µÄĆ껿£»
£Ø2£©ŗĻ×÷½»Į÷£ŗ”°Ļ£Ķū”±Š”×éŹÜĪŹĢā£Ø1£©µÄĘō·¢£¬½«”÷DEFČʵćDŠż×Ŗ£¬Ź¹DE”ĶAB½»ACÓŚµćH£¬DF½»ACÓŚµćG£¬ČēĶ¼2£¬ĒóÖŲµž²æ·Ö£Ø”÷DGH£©µÄĆ껿£®
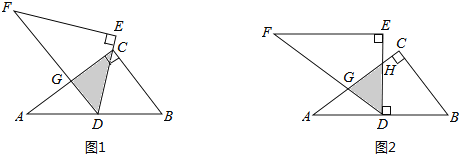
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢµźŅŖŌĖŅ»Åś»õĪļ£¬×āÓĆ¼×”¢ŅŅĮ½³µŌĖĖĶ£®ČōĮ½³µŗĻ×÷£¬ø÷ŌĖ12ĢĖ²ÅÄÜĶź³É£¬ŠčÖ§ø¶ŌĖ·Ń¹²4800ŌŖ£»Čō¼×”¢ŅŅĮ½³µµ„¶ĄŌĖĶźÕāÅś»õĪļ£¬ŌņŅŅ³µĖłŌĖĢĖŹżŹĒ¼×³µµÄ2±¶£»ŅŃÖŖŅŅ³µ°ĢĖŌĖ·Ń±Č¼×³µÉŁ200ŌŖ£®
£Ø1£©·Ö±šĒó³ö¼×”¢ŅŅĮ½³µĆæĢĖµÄŌĖ·Ń£»
£Ø2£©Čōµ„¶Ą×āÓĆ¼×³µŌĖĶź“ĖÅś»õĪļ£¬ŠčŌĖ¶ąÉŁĢĖ£»
£Ø3£©ČōĶ¬Ź±×āÓĆ¼×”¢ŅŅĮ½³µ£¬Ōņ¼×³µŌĖxĢĖ£¬ŅŅ³µŌĖyĢĖ£¬²ÅÄÜŌĖĶź“ĖÅś»õĪļ£¬ĘäÖŠx”¢y¾łĪŖÕżÕūŹż£¬Éč×ÜŌĖ·ŃĪŖw£ØŌŖ£©£¬ĒówÓėxµÄŗÆŹż¹ŲĻµŹ½£¬Ö±½ÓŠ“³öwµÄ×īŠ”Öµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
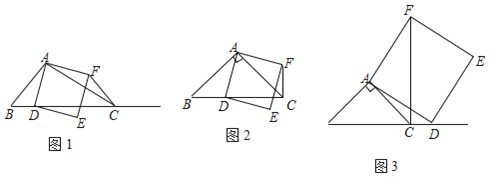
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() ĪŖČń½Ē£¬µć
ĪŖČń½Ē£¬µć![]() ĪŖÉäĻß
ĪŖÉäĻß![]() ÉĻŅ»µć£¬ĮŖ½į
ÉĻŅ»µć£¬ĮŖ½į![]() £¬ŅŌ
£¬ŅŌ![]() ĪŖŅ»±ßĒŅŌŚ
ĪŖŅ»±ßĒŅŌŚ![]() µÄÓŅ²ą×÷Õż·½ŠĪ
µÄÓŅ²ą×÷Õż·½ŠĪ![]() £®
£®
£Ø1£©Čē¹ū![]() £¬
£¬![]() £¬
£¬
¢Łµ±µć![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī![]() ÉĻŹ±£ØÓėµć
ÉĻŹ±£ØÓėµć![]() ²»ÖŲŗĻ£©£¬ČēĶ¼2£¬Ļ߶Ī
²»ÖŲŗĻ£©£¬ČēĶ¼2£¬Ļ߶Ī![]() ĖłŌŚÖ±ĻßµÄĪ»ÖĆ¹ŲĻµĪŖ £¬Ļ߶Ī
ĖłŌŚÖ±ĻßµÄĪ»ÖĆ¹ŲĻµĪŖ £¬Ļ߶Ī![]() µÄŹżĮæ¹ŲĻµĪŖ £»
µÄŹżĮæ¹ŲĻµĪŖ £»
¢Śµ±µć![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī![]() µÄŃÓ³¤ĻßÉĻŹ±£¬ČēĶ¼3£¬¢ŁÖŠµÄ½įĀŪŹĒ·ńČŌČ»³ÉĮ¢£¬²¢ĖµĆ÷ĄķÓÉ£»
µÄŃÓ³¤ĻßÉĻŹ±£¬ČēĶ¼3£¬¢ŁÖŠµÄ½įĀŪŹĒ·ńČŌČ»³ÉĮ¢£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©Čē¹ū![]() £¬
£¬![]() ŹĒČń½Ē£¬µć
ŹĒČń½Ē£¬µć![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī![]() ÉĻ£¬µ±
ÉĻ£¬µ±![]() Āś×ćŹ²Ć“Ģõ¼žŹ±£¬
Āś×ćŹ²Ć“Ģõ¼žŹ±£¬![]() £Øµć
£Øµć![]() ²»ÖŲŗĻ£©£¬²¢ĖµĆ÷ĄķÓÉ£®
²»ÖŲŗĻ£©£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com