
【题目】如图,在△ABC中,AC=BC,AD平分∠BAC,∠ADC=60°,求∠C的度数.

【答案】100°
【解析】试题设∠BAD=x.由AD平分∠BAC,得出∠CAD=∠BAD=x,∠BAC=2∠BAD=2x.由AC=BC,得出∠B=∠BAC=2x.根据三角形外角的性质得出∠ADC=∠B+∠BAD=60°,即2x+x=60°,求得x=20°,那么∠B=∠BAC=40°.然后在△ABC中,根据三角形内角和定理得出∠C=180°-∠B-∠BAC=100°.
试题解析:设∠BAD=x.
∵AD平分∠BAC,
∴∠CAD=∠BAD=x,∠BAC=2∠BAD=2x.
∵AC=BC,
∴∠B=∠BAC=2x.
∵∠ADC=∠B+∠BAD=60°,
∴2x+x=60°,
∴x=20°,
∴∠B=∠BAC=40°.
在△ABC中,∵∠BAC+∠B+∠C=180°,
∴∠C=180°-∠B-∠BAC=100°.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
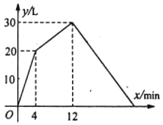
【题目】一个装有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单价:min)之间的关系如图所示。在第_______分钟时该容器内的水恰好为10L.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1: ![]() ,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC= .
,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC= . 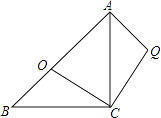
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+ ![]() 与y轴相交于点A,点B与点O关于点A对称.
与y轴相交于点A,点B与点O关于点A对称. 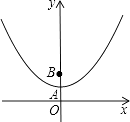
(1)填空:点B的坐标为;
(2)过点B的直线y=kx+b(其中k<0)与x轴相交于点C,过点C作直线l平行于y轴,P是直线l上一点,且PB=PC,求线段PB的长(用含k的式子表示),并判断点P是否在抛物线上,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
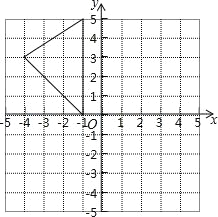
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
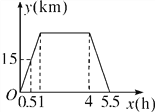
【题目】周末,小李从家里出发骑车到少年宫学习绘画,学完后立即回家,他离家的距离y(km)与时间x(h)之间的函数关系如图所示,有下列结论:①他家离少年宫30km;②他在少年宫一共停留了3h;③他返回家时,离家的距离y(km)与时间x(h)之间的函数表达式是y=-20x+110;④当他离家的距离y=10时,时间x=![]() .其中正确的是________(填序号).
.其中正确的是________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知点A(4-a,-2a-3)和点B(-2,5),且AB∥x轴,试求点A的坐标;
(2)把点P(m+1,n-2m)先向右平移4个单位长度,再向下平移6个单位长度后得到点P′的坐标为(3,-2),试求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地A、B两村盛产柑橘,A村有柑橘200吨,B村有柑橘300吨,现将这些柑橘运到C、D两个冷藏仓库.已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为每吨20元、25元,从B村运往C、D两处的费用分别为每吨15元、18元.设从A村运往C仓库的柑橘重量为x吨,A、B两村运往两仓库的柑橘运输费用分别为yA元、yB元.
(1)请填写下表,并求出yA、yB与x之间的函数表达式;

(2)试讨论A、B两村中,哪个村的运费较少;
(3)考虑到B村的经济承受能力,B村的柑橘运费不得超过4830元,在这种情况下,请问怎样调运才能使两村运费之和最小?求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数按要求分类:
![]()
负整数集合:{____________________}
正分数集合:{____________________}
负分数集合:{____________________}
整数集合:{_______________________}
负有理数集合:{_______________________}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com