
 如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′=46度.
如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′=46度. 分析 先根据三角形外角的性质求出∠ACA′=67°,再由△ABC绕点C按顺时针方向旋转至△A′B′C,得到△ABC≌△A′B′C,证明∠BCB′=∠ACA′,利用平角即可解答.
解答 解:∵∠A=27°,∠B=40°,
∴∠ACA′=∠A+∠B=27°+40°=67°,
∵△ABC绕点C按顺时针方向旋转至△A′B′C,
∴△ABC≌△A′B′C,
∴∠ACB=∠A′CB′,
∴∠ACB-∠B′CA=∠A′CB-∠B′CA,
即∠BCB′=∠ACA′,
∴∠BCB′=67°,
∴∠ACB′=180°-∠ACA′-∠BCB′=180°-67°-67°=46°,
故答案为:46.
点评 本题考查了旋转的性质,解决本题的关键是由旋转得到△ABC≌△A′B′C.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:选择题
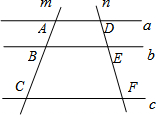 如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{EF}$=( )
如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{EF}$=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
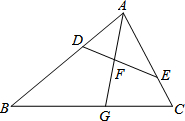 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且$\frac{AD}{AC}=\frac{DF}{CG}$.
如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且$\frac{AD}{AC}=\frac{DF}{CG}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 开口向上 | B. | 与x轴有两个重合的交点 | ||
| C. | 对称轴是直线x=1 | D. | 当x>1时,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.2 | B. | 0.4 | C. | 0.6 | D. | 0.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com