
【题目】如图,将△ABC绕点C顺时针旋转m°得到△EDC,若点A、D、E在同一直线上,∠ACB=n°,则∠ADC的度数是( )

A. (m﹣n)°B. (90+n-![]() m)°C. (90-
m)°C. (90-![]() n+m)°D. (180﹣2n﹣m)°
n+m)°D. (180﹣2n﹣m)°
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]()

(1)画出![]() 的
的![]() 边上的高CH;
边上的高CH;
(2)将![]() 平移到
平移到![]() (点
(点![]() 和点
和点![]() 对应,点
对应,点![]() 和点
和点![]() 对应,点
对应,点![]() 和点
和点![]() 对应),若点
对应),若点![]() 的坐标为
的坐标为![]() ,请画出平移后的
,请画出平移后的![]() ;
;
(3)若![]() ,
,![]() 为平面内一点,且满足
为平面内一点,且满足![]() 与
与![]() 全等,请直接写出点
全等,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)拼一拼,画一画:请你用4个长为a,宽为b的矩形拼成一个大正方形,并且正中间留下一个洞,这个洞恰好是一个小正方形。

(2)用不同方法计算中间的小正方形的面积,聪明的你能发现什么?
(3)当拼成的这个大正方形边长比中间小正方形边长多3cm时,它的面积就多24cm2,求中间小正方形的边长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P是AB的中点,![]() 的延长线于点E,连接AE,过点A作
的延长线于点E,连接AE,过点A作![]() 交DP于点F,连接BF、
交DP于点F,连接BF、![]() 下列结论中:
下列结论中:![]() ≌
≌![]() ;
;![]() ;
;![]() 是等边三角形;
是等边三角形;![]() ;
;![]() 其中正确的是
其中正确的是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
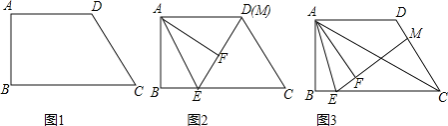
(1)如图1,连接AC,求证:CA是![]() 的平分线;
的平分线;
(2)线段BC上一点E,将![]() 沿AE翻折,点B落到点F处,射线EF与线段CD交于点M.
沿AE翻折,点B落到点F处,射线EF与线段CD交于点M.
①如图2,当点M与点D重合时,求证:![]() ;
;
②如图3,当点M不与点D重合时,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比学习:
一动点沿着数轴向右平移![]() 个单位,再向左平移
个单位,再向左平移![]() 个单位,相当于向右平移
个单位,相当于向右平移![]() 个单位.用有理数加法表示为
个单位.用有理数加法表示为![]() .若坐标平面上的点做如下平移:沿
.若坐标平面上的点做如下平移:沿![]() 轴方向平移的数量为
轴方向平移的数量为![]() (向右为正,向左为负,平移
(向右为正,向左为负,平移![]() 个单位),沿
个单位),沿![]() 轴方向平移的数量为
轴方向平移的数量为![]() (向上为正,向下为负,平移
(向上为正,向下为负,平移![]() 个单位),则把有序数对
个单位),则把有序数对![]() 叫做这一平移的“平移量”;“平移量”
叫做这一平移的“平移量”;“平移量”![]() 与“平移量”
与“平移量”![]() 的加法运算法则为
的加法运算法则为![]()
解决问题:
(1)计算:![]() ;
;
(2)动点![]() 从坐标原点
从坐标原点![]() 出发,先按照“平移量”
出发,先按照“平移量”![]() 平移到
平移到![]() ,再按照“平移量”
,再按照“平移量”![]() 平移到
平移到![]() :若先把动点
:若先把动点![]() 按照.“平移量”
按照.“平移量”![]() 平移到
平移到![]() ,再按照“平移量”
,再按照“平移量”![]() 平移,最后的位置还是
平移,最后的位置还是![]() 吗?在图1中画出四边形
吗?在图1中画出四边形![]() .
.
(3)如图2,一艘船从码头![]() 出发,先航行到湖心岛码头
出发,先航行到湖心岛码头![]() ,再从码头
,再从码头![]() 航行到码头
航行到码头![]() ,最后回到出发点
,最后回到出发点![]() .请用“平移量”加法算式表示它的航行过程.
.请用“平移量”加法算式表示它的航行过程.


解:(1)![]() ______;
______;
(2)答:______;
(3)加法算式:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简:
(1)2﹣1+![]()
(2)2x2y(﹣3xy)÷(xy)2
(3)(﹣2a)(3a2﹣a+3)
(4)(x+3)(x+4)﹣(x﹣1)2
(5)[2a3x2(a﹣2x)﹣![]() a2x2]÷(﹣ax)2
a2x2]÷(﹣ax)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,a),将线段OA平移至线段BC,B(b,0),a是m+6n的算术平方根,![]() =3,n=
=3,n=![]() ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.
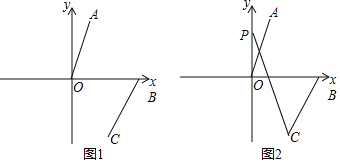
(1)直接写出A、B两点坐标为:A ,B ;
(2)如图1,连接AB、OC,求四边形AOCB的面积;
(3)如图2,若∠AOB=a,点P为y轴正半轴上一动点,试探究∠CPO与∠BCP之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABF中,∠F=90°,点C是线段BF上异于点B和点F的一点,连接AC,过点C作CD⊥AC交AB于点D,过点C作CE⊥AB交AB于点E,则下列说法中,错误的是( )

A.△ABC中,AB边上的高是CEB.△ABC中,BC边上的高是AF
C.△ACD中,AC边上的高是CED.△ACD中,CD边上的高是AC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com