
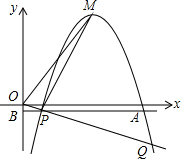
 如图,在平面直角坐标系xOy中,点M为抛物线y=-x2+2nx-n2+2n(n>2)的顶点,直线y=-$\frac{1}{2}$x与抛物线交于点P、Q,过点P作PA∥x轴,交抛物线于另一点A,交y轴于点B.
如图,在平面直角坐标系xOy中,点M为抛物线y=-x2+2nx-n2+2n(n>2)的顶点,直线y=-$\frac{1}{2}$x与抛物线交于点P、Q,过点P作PA∥x轴,交抛物线于另一点A,交y轴于点B.分析 (1)把抛物线解析式配成顶点式即可得到M点坐标;
(2)设P(t,-$\frac{1}{2}$t),而M(n,2n),利用两点间的距离公式得到OM2=5n2,OP2=$\frac{5}{4}$t2,NP2=5n2+$\frac{5}{4}$t2,然后利用勾股定理的逆定理可证明△OMP为直角三角形,∠MOP=90°,于是可判断OM⊥OP;
(3)作QK⊥x轴于K,如图,证明△OMN≌△QOK得到OK=MN=2n,ON=QK=n,则Q(2n,-n),利用二次函数图象上点的坐标特征得到-4n2+4n-n2+2n=-n,解得n1=0,n2=3,于是得到n=3;
(4)由(2)得P(t,-$\frac{1}{2}$t),M(n,2n),OM=$\sqrt{5}$n,OP=$\frac{\sqrt{5}}{2}$t,作MN⊥AB于N点,如图,则NP=NA=n-t,利用三角形面积公式得到$\frac{1}{2}$•2(n-t)•(2n+$\frac{1}{2}$t)=2•$\frac{1}{2}$•$\sqrt{5}$n•$\frac{\sqrt{5}}{2}$t,解得n1=$\frac{2+\sqrt{5}}{2}$t,n2=$\frac{2-\sqrt{5}}{2}$t(舍去),即n=$\frac{2+\sqrt{5}}{2}$t,然后在Rt△OMP中,利用正切的定义求解.
解答 (1)解:∵y=-x2+2nx-n2+2n=-(x-n)2+2n,
∴M(n,2n);
(2)证明:设P(t,-$\frac{1}{2}$t),而M(n,2n),
∴OM2=n2+(2n)2=5n2,OP2=t2+($\frac{1}{2}$t)2=$\frac{5}{4}$t2,NP2=(n-t)2+(2n+$\frac{1}{2}$t)2=5n2+$\frac{5}{4}$t2,
∴OM2+OP2=NP2,
∴△OMP为直角三角形,∠MOP=90°,
∴OM⊥OP;
(3)解:作QK⊥x轴于K,如图,
∵∠MOQ=90°,即∠MON+∠QOK=90°,
而∠MON+∠OMN=90°,
∴∠OMN=∠QOK,
在△OMN和△QOK中
$\left\{\begin{array}{l}{∠ONM=∠QKO}\\{∠OMN=∠QOK}\\{OM=QO}\end{array}\right.$,
∴△OMN≌△QOK,
∴OK=MN=2n,ON=QK=n,
∴Q(2n,-n),
∵Q(2n,-n)在抛物线y=-x2+2nx-n2+2n上,
∴-4n2+4n-n2+2n=-n,解得n1=0,n2=3,
而n>2,
∴n=3;
(4)解:P(t,-$\frac{1}{2}$t),M(n,2n),OM=$\sqrt{5}$n,OP=$\frac{\sqrt{5}}{2}$t,
作MN⊥AB于N点,如图,则NP=NA=n-t,
∵△MPA的面积是△POM面积的2倍,
∴$\frac{1}{2}$•2(n-t)•(2n+$\frac{1}{2}$t)=2•$\frac{1}{2}$•$\sqrt{5}$n•$\frac{\sqrt{5}}{2}$t,
整理得4n2-8nt-t2=0,解得n1=$\frac{2+\sqrt{5}}{2}$t,n2=$\frac{2-\sqrt{5}}{2}$t(舍去),
即n=$\frac{2+\sqrt{5}}{2}$t,
在Rt△OMP中,tan∠OPM=$\frac{OM}{OP}$=$\frac{\sqrt{5}n}{\frac{\sqrt{5}t}{2}}$=$\frac{2n}{t}$=2+$\sqrt{5}$.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和勾股定理的逆定理;理解坐标与图形性质,会运用两点间的距离公式计算线段的长;会运用全等三角形证明线段相等.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题
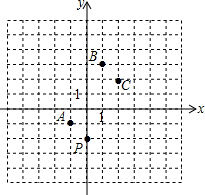 如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点K处…如此继续下去.
如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点K处…如此继续下去.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
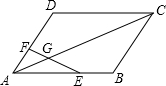 如图,在?ABCD中,E是AB的中点,点F在AD上,且$\frac{AF}{FD}$=$\frac{1}{2}$,EF交AC于点G,求$\frac{AG}{GC}$的值.
如图,在?ABCD中,E是AB的中点,点F在AD上,且$\frac{AF}{FD}$=$\frac{1}{2}$,EF交AC于点G,求$\frac{AG}{GC}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,正六边形ABCDEF的边长为6cm.延长FE,CD相交于点G.
已知:如图,正六边形ABCDEF的边长为6cm.延长FE,CD相交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
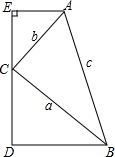 如图,在四边形ABDE中,∠E=90°,AE∥BD,C为ED上一点,设△ABC三边分别为a、b、c,且方程(a+c)x2-2bx-a+c=0有两相等实根.
如图,在四边形ABDE中,∠E=90°,AE∥BD,C为ED上一点,设△ABC三边分别为a、b、c,且方程(a+c)x2-2bx-a+c=0有两相等实根.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com