
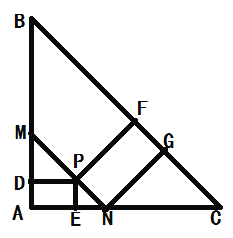
【题目】在△ABC 中,∠A=90°,AB=AC=![]() +1,P 是△ABC 内一个动点,PD⊥AB、PE⊥AC、PF⊥BC,垂足分别为 D、E、F,且 PD+PE=PF.则点 P 运动所形成的图形的长度是__________.
+1,P 是△ABC 内一个动点,PD⊥AB、PE⊥AC、PF⊥BC,垂足分别为 D、E、F,且 PD+PE=PF.则点 P 运动所形成的图形的长度是__________.
【答案】![]()
【解析】如图,过点P作MN∥BC,交AB于点M,交BC于点N,由PD⊥AB、PE⊥AC、∠A=90°,可得四边形AEPD为矩形,所以DP=AE;由∠A=90°,AB=AC=![]() +1,可得∠C=45°,再由MN∥BC,PE⊥AC可得△PEN为等腰直角三角形,所以PE=EN;又因PD+PE=PF,可得PF=AE+EN=AN;过点N作NG⊥BC与点G,可得PF=EG,△CGN为等腰直角三角形,设PF=EG=x,可得NG=
+1,可得∠C=45°,再由MN∥BC,PE⊥AC可得△PEN为等腰直角三角形,所以PE=EN;又因PD+PE=PF,可得PF=AE+EN=AN;过点N作NG⊥BC与点G,可得PF=EG,△CGN为等腰直角三角形,设PF=EG=x,可得NG=![]() x,因为AC=
x,因为AC=![]() +1,所以AN+NG=x+
+1,所以AN+NG=x+![]() x=
x=![]() +1,解得x=1;由此可得当PD+PE=PF时,点 P 运动所形成的图形是线段MN,根据勾股定理可求得MN的长度为
+1,解得x=1;由此可得当PD+PE=PF时,点 P 运动所形成的图形是线段MN,根据勾股定理可求得MN的长度为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图2,“和谐号”高铁列车的小桌板收起时近似看作与地面垂直,展开小桌板使桌面保持水平时如图1,小桌板的边沿O点与收起时桌面顶端A点的距离OA=75厘米,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与支架长BC的长度之和等于OA的长度. 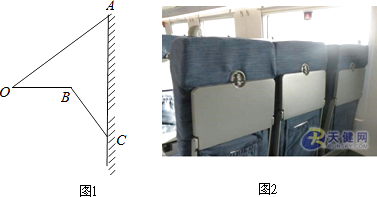
(1)求∠CBO的度数;
(2)求小桌板桌面的宽度BC.(参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱我中华”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:甲:8,7,9,8,8;乙:7,9,6,9,9,则下列说法中错误的是( )
A. 甲、乙得分的平均数都是8 B. 甲得分的众数是8,乙得分的众数是9
C. 甲得分的中位数是9,乙得分的中位数是6 D. 甲得分的方差比乙得分的方差小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如![]() 善于思考的小明进行了以下探索:
善于思考的小明进行了以下探索:
设![]() 其中a、b、m、n均为整数
其中a、b、m、n均为整数![]() ,则有
,则有![]() .
.
![]() 这样小明就找到了一种把类似
这样小明就找到了一种把类似![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
![]() 当a、b、m、n均为正整数时,若
当a、b、m、n均为正整数时,若![]() ,用含m、n的式子分别表示a、b,得:
,用含m、n的式子分别表示a、b,得: ![]() ______,
______, ![]() ______;
______;
![]() 利用所探索的结论,请找一组正整数a、b、m、n填空:
利用所探索的结论,请找一组正整数a、b、m、n填空:
______![]() _____
_____![]() ______
______![]()
______![]() ;
;
![]() 若
若![]() 且a、m、n均为正整数,求a的值.
且a、m、n均为正整数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
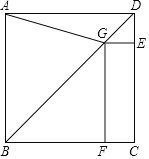
【题目】如图,在正方形ABCD中,点G在对角线BD上![]() 不与点
不与点![]() 重合
重合![]() 于点
于点![]() 于点F,连结AG.
于点F,连结AG.
![]() 写出线段
写出线段![]() 长度之间的数量关系,并说明理由;
长度之间的数量关系,并说明理由;
![]() 若正方形ABCD的边长为
若正方形ABCD的边长为![]() ,求线段BG的长.
,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) | n=50﹣x |
销售单价m(元/件) | 当1≤x≤20时,m=20+ |
当21≤x≤30时,m=10+ |
(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一单位长度为1cm的方格纸上,依如图所示的规律,设定点A1、A2、A3、A4、A5、A6、A7、…、An,连接点O、A1、A2组成三角形,记为△1,连接O、A2、A3组成三角形,记为△2…,连O、An、An+1组成三角形,记为△n(n为正整数),请你推断,当n为50时,△n的面积=( )cm2.
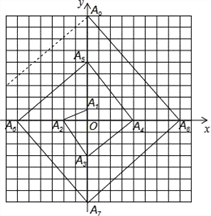
A. 1275 B. 2500 C. 1225 D. 1250
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交AB于M,交DC于N.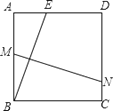
(1)设AE=x,四边形ADNM的面积为S,写出S关于x的函数关系式;
(2)当AE为何值时,四边形ADNM的面积最大?最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com