
【题目】我们不妨约定:如图①,若点D在△ABC的边AB上,且满足∠ACD=∠B(或∠BCD=∠A),则称满足这样条件的点为△ABC边AB上的“理想点”.
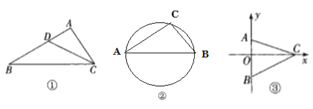
(1)如图①,若点D是△ABC的边AB的中点,AC=![]() ,AB=4.试判断点D是不是△ABC边AB上的“理想点”,并说明理由.
,AB=4.试判断点D是不是△ABC边AB上的“理想点”,并说明理由.
(2)如图②,在⊙O中,AB为直径,且AB=5,AC=4.若点D是△ABC边AB上的“理想点”,求CD的长.
(3)如图③,已知平面直角坐标系中,点A(0,2),B(0,-3),C为x轴正半轴上一点,且满足∠ACB=45°,在y轴上是否存在一点D,使点A是B,C,D三点围成的三角形的“理想点”,若存在,请求出点D的坐标;若不存在,请说明理由.
【答案】(1)是,理由见解析;(2)![]() ;(3)D(0,42)或D(0,6)
;(3)D(0,42)或D(0,6)
【解析】
(1)依据边长AC=![]() ,AB=4,D是边AB的中点,得到AC2=
,AB=4,D是边AB的中点,得到AC2=![]() ,可得到两个三角形相似,从而得到∠ACD=∠B;
,可得到两个三角形相似,从而得到∠ACD=∠B;
(2)由点D是△ABC的“理想点”,得到∠ACD=∠B或∠BCD=∠A,分两种情况证明均得到CD⊥AB,再根据面积法求出CD的长;
(3)使点A是B,C,D三点围成的三角形的“理想点”,应分两种情况讨论,利用三角形相似分别求出点D的坐标即可.
(1)D是△ABC边AB上的“理想点”,理由:
∵AB=4,点D是△ABC的边AB的中点,
∴AD=2,
∵AC2=8,![]() ,
,
∴AC2=![]() ,
,
又∵∠A=∠A,
∴△ADC∽△ACB,
∴∠ACD=∠B,
∴D是△ABC边AB上的“理想点”.
(2)如图②,

∵点D是△ABC的“理想点”,
∴∠ACD=∠B或∠BCD=∠A,
当∠ACD=∠B时,
∵∠ACD+∠BCD=90![]() ,
,
∴∠BCD+∠B=90![]() ,
,
∴∠CDB=90![]() ,
,
当∠BCD=∠A时,同理可得CD⊥AB,
在Rt△ABC中,∵∠ACB=90![]() ,AB=5,AC=4,
,AB=5,AC=4,
∴BC=![]() =3,
=3,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)如图③,存在.
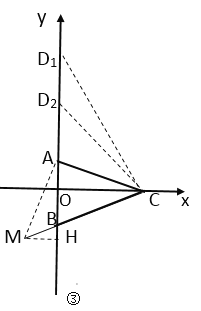
过点A作MA⊥AC交CB的延长线于点M,∵∠MAC=∠AOC=90![]() ,∠ACM=45
,∠ACM=45![]() ,
,
∴∠AMC=∠ACM=45![]() ,
,
∴AM=AC,
∵∠MAH+∠CAO=90![]() ,∠CAO+∠ACO=90
,∠CAO+∠ACO=90![]() ,
,
∴∠MAH=∠ACO,
∴△AHM≌△COA
∴MH=OA,OC=AH,
设C(a,0),
∵A(0,2),B(0,-3),
∴OA=MH=2,OB=3,AB=5,OC=AH=a,BH=a-5,
∵MH∥OC,
∴![]() ,
,
∴![]() ,
,
解得a=6或a=-1(舍去),
经检验a=6是原分式方程的解,
∴C(6,0),OC=6.
①当∠D1CA=∠ABC时,点A是△BCD1的“理想点”,
设D1(0,m),
∵∠D1CA=∠ABC,∠CD1A=∠CD1B,
∴△D1AC∽△D1CB,
∴![]() ,
,
∴![]() ,
,
解得m=42,∴D1(0,42);
②当∠BCA=∠CD2B时,点A是△BCD2“理想点”,
可知:∠CD2O=45![]() ,
,
∴OD2=OC=6,
∴D2(0,6).
综上,满足条件的点D的坐标为D(0,42)或D(0,6).


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
(1)试求取出的两张卡片数字之和为奇数的概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B的坐标分别为(0,8),(10,0),动点C,D分别在OA,OB上且CD=8,以CD为直径作⊙P交AB于点E,F.动点C从点O向终点A的运动过程中,线段EF长的变化情况为( )
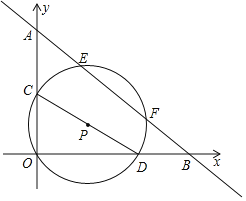
A.一直不变B.一直变大
C.先变小再变大D.先变大再变小
查看答案和解析>>
科目:初中数学 来源: 题型:
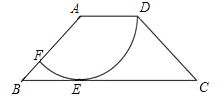
【题目】如图,在四边形ABCD中,AD∥BC,AD=2,AB=![]() ,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
(1)求∠ABE的大小及![]() 的长度;
的长度;
(2)在BE的延长线上取一点G,使得![]() 上的一个动点P到点G的最短距离为
上的一个动点P到点G的最短距离为![]() ,求BG的长.
,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
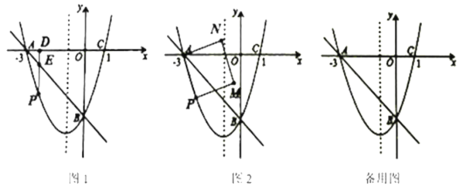
【题目】如图1,抛物线y = ax2+bx-3经过A、B、C三点,己知点A(-3,0)、C (1, 0).
(1)求此抛物线的解析式.
(2)点P是直线AB下方的抛物线上一动点(不与A、B重合),
①过点F作x轴的垂线,垂足为D,交直线AB于点E,动点P在什么位置时,PE最大,求 出此时P点的坐标.
②如图2,连接AP.以AP为边作图示一侧的正方形APMN,当它恰好有一个顶点落在抛物 线对称轴上时,求出对应的P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
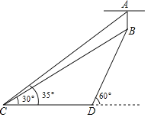
【题目】如图,宾馆大厅的天花板上挂有一盏吊灯AB,某人从C点测得吊灯顶端A的仰角为![]() ,吊灯底端B的仰角为
,吊灯底端B的仰角为![]() ,从C点沿水平方向前进6米到达点D,测得吊灯底端B的仰角为
,从C点沿水平方向前进6米到达点D,测得吊灯底端B的仰角为![]() .请根据以上数据求出吊灯AB的长度.(结果精确到0.1米.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,
.请根据以上数据求出吊灯AB的长度.(结果精确到0.1米.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题:
如图,已知线段AB,BC,∠ABC = 90°. 求作:矩形ABCD.

小明的作图过程如下:
(1)连接AC,作线段AC的垂直平分线,交AC于M;
(2)连接BM并延长,在延长线上取一点D,使MD=MB,连接AD,CD.
∴四边形ABCD即为所求.

老师说:“小明的作法正确.”
请回答:小明这样作图的依据是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学不仅是一门学科,也是一种文化,即数学文化.数学文化包括数学史、数学美和数学应用等多方面.古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋,为了对聪明的大臣表示感谢,国王答应满足这位大臣的一个要求.大臣说:“就在这个棋盘上放一些米粒吧.第![]() 格放
格放![]() 粒米,第
粒米,第![]() 格放
格放![]() 粒米,第
粒米,第![]() 格放
格放![]() 粒米,然后是
粒米,然后是![]() 粒、
粒、![]() 粒、
粒、![]() 粒······一只到第
粒······一只到第![]() 格.”“你真傻!就要这么一点米粒?”国王哈哈大笑.大臣说:“就怕您的国库里没有这么多米!”国王的国库里真没有这么多米吗?题中问题就是求
格.”“你真傻!就要这么一点米粒?”国王哈哈大笑.大臣说:“就怕您的国库里没有这么多米!”国王的国库里真没有这么多米吗?题中问题就是求![]() 是多少?请同学们阅读以下解答过程就知道答案了.
是多少?请同学们阅读以下解答过程就知道答案了.
设![]() ,
,
则![]()
![]()
![]()
即:![]()
事实上,按照这位大臣的要求,放满一个棋盘上的![]() 个格子需要
个格子需要![]() 粒米.那么
粒米.那么![]() 到底多大呢?借助计算机中的计算器进行计算,可知答案是一个
到底多大呢?借助计算机中的计算器进行计算,可知答案是一个![]() 位数:
位数:![]()
![]() ,这是一个非常大的数,所以国王是不能满足大臣的要求.请用你学到的方法解决以下问题:
,这是一个非常大的数,所以国王是不能满足大臣的要求.请用你学到的方法解决以下问题:
![]() 我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座
我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座![]() 层塔共挂了
层塔共挂了![]() 盏灯,且相邻两层中的下一层灯数是上一层灯数的
盏灯,且相邻两层中的下一层灯数是上一层灯数的![]() 倍,则塔的顶层共有多少盏灯?
倍,则塔的顶层共有多少盏灯?
![]() 计算:
计算: ![]()
![]() 某中学“数学社团”开发了一款应用软件,推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:
某中学“数学社团”开发了一款应用软件,推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:
已知一列数:![]() ,其中第一项是
,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,以此类推,求满足如下条件的所有正整数
,以此类推,求满足如下条件的所有正整数![]() ,且这一数列前
,且这一数列前![]() 项和为
项和为![]() 的正整数幂.请直接写出所有满足条件的软件激活码正整数
的正整数幂.请直接写出所有满足条件的软件激活码正整数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
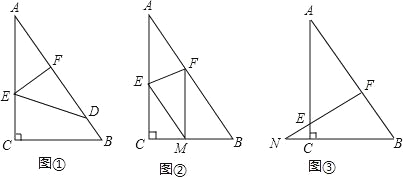
【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.
(1)图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长;
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com