练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    将图形中的△ABC分别作下列移动，画出相应的图形，指出三个顶点的坐标所发生的变化．

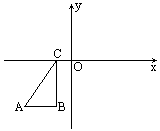
    (1)向上平移4个单位；

    (2)关于y轴成轴对称；

    (3)以A点为位似中心，放大到2倍．

    答案：
    解析：

    　　答案：如图，(1)平移后得△A1B1C1，横坐标不变，纵坐标都加4．

    　　(2)△ABC关于y轴对称的图形为△A2B2C2，纵坐标不变，横坐标为对应点横坐标的相反数．

    　　(3)放大后得△AB2C3，A的坐标当然不变，B2在B的基础上纵坐标不变，横坐标加AB的长，C3的横坐标加AB的长，纵坐标加BC的长．

    　　剖析：(1)向上平移4个单位，则是沿y轴的正方向平移4个单位，则横坐标不变，而纵坐标应该加4．

    　　(2)一个图形关于y轴对称，则纵坐标不变，发生变化的是横坐标，变为对应点横坐标的相反数．

    　　(3)以A点为位似中心，放大到2倍，则放大后的图形，A点的坐标不变，而B，C的对应点的坐标则发生变化，相当于是AB、BC的长度扩大2倍来确定点的坐标．


    提示：

    图形在平面直角坐标系中移动，则坐标会发生一定的变化，要注意哪些变，哪些不变．作位似变化时，只要求表示出顶点坐标即可，其他不作太高的要求．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （如图1），点P将线段AB分成一条较小线段AP和一条较大线段BP，如果
    AP
    BP
    =
    BP
    AB
    ，那么称点P为线段AB的黄金分割点，设
    AP
    BP
    =
    BP
    AB
    =k，则k就是黄金比，并且k≈0.618．
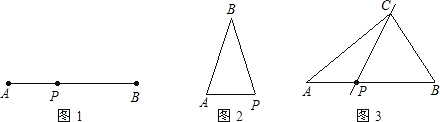
    精英家教网
    （1）以图1中的AP为底，BP为腰得到等腰△APB（如图2），等腰△APB即为黄金三角形，黄金三角形的定义为：满足
    底
    腰
    =
    腰
    底+腰
    ≈0.618的等腰三角形是黄金三角形；类似地，请你给出黄金矩形的定义：
     
    ；
    （2）如图1，设AB=1，请你说明为什么k约为0.618；
    （3）由线段的黄金分割点联想到图形的“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分（设S1＜S2），如果
    S1
    S2
    =
    S2
    S
    ，那么称直线l为该图形的黄金分割线．（如图3），点P是线段AB的黄金分割点，那么直线CP是△ABC的黄金分割线吗？请说明理由；
    （4）图3中的△ABC的黄金分割线有几条？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    22、如图1，若将△AOB绕点O逆时针旋转180°得到△COD，则△AOB≌△COD．此时，我们称△AOB与△COD为“8字全等型”．借助“8字全等型”我们可以解决一些图形的分割与拼接问题．例如：图2中，△ABC是锐角三角形且AC＞AB，点E为AC中点，F为BC上一点且BF≠FC（F不与B，C重合），沿EF将其剪开，得到的两块图形恰能拼成一个梯形．
    请分别按下列要求用直线将图2中的△ABC重新进行分割，画出分割线及拼接后的图形．
    （1）在图3中将△ABC沿分割线剪开，使得到的两块图形恰能拼成一个平行四边形；
    （2）在图4中将△ABC沿分割线剪开，使得到的三块图形恰能拼成一个矩形，且其中的两块为直角三角形；
    （3）在图5中将△ABC沿分割线剪开，使得到的三块图形恰能拼成一个矩形，且其中的一块为钝角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，若将△AOB绕点O逆时针旋转180°得到△COD，则△AOB≌△COD．此时，我们称△AOB与△COD为“8字全等型”．借助“8字全等型”我们可以解决一些图形的分割与拼接问题．例如：图2中，△ABC是锐角三角形且AC＞AB，点E为AC中点，F为BC上一点且BF≠FC（F不与B、C重合），沿EF将其剪开，得到的两块图形恰能拼成一个梯形．

    请分别按下列要求用直线将图2中的△ABC重新进行分割，画出分割线及拼接后的图形．

    【小题1】（1）在图3中将△ABC沿分割线剪开，使得到的两块图形恰能拼成一个平行四边形；
    【小题2】（2在图4中将△ABC沿分割线剪开，使得到的三块图形恰能拼成一个矩形，且其中的两块为直角三角形；
    【小题3】（3在图5中将△ABC沿分割线剪开，使得到的三块图形恰能拼成一个矩形，且其中的一块为锐角三角形．

    查看答案和解析>>

    科目：初中数学 来源：2012届北京市延庆县九年级上学期期末考试数学卷 题型：解答题

    如图1，若将△AOB绕点O逆时针旋转180°得到△COD，则△AOB≌△COD．此时，我们称△AOB与△COD为“8字全等型”．借助“8字全等型”我们可以解决一些图形的分割与拼接问题．例如：图2中，△ABC是锐角三角形且AC＞AB，点E为AC中点，F为BC上一点且BF≠FC（F不与B、C重合），沿EF将其剪开，得到的两块图形恰能拼成一个梯形．

    请分别按下列要求用直线将图2中的△ABC重新进行分割，画出分割线及拼接后的图形．

    【小题1】（1）在图3中将△ABC沿分割线剪开，使得到的两块图形恰能拼成一个平行四边形；
    【小题2】（2在图4中将△ABC沿分割线剪开，使得到的三块图形恰能拼成一个矩形，且其中的两块为直角三角形；
    【小题3】（3在图5中将△ABC沿分割线剪开，使得到的三块图形恰能拼成一个矩形，且其中的一块为锐角三角形．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年北京市延庆县九年级上学期期末考试数学卷 题型：解答题

     如图1，若将△AOB绕点O逆时针旋转180°得到△COD，则△AOB≌△COD．此时，我们称△AOB与△COD为“8字全等型”．借助“8字全等型”我们可以解决一些图形的分割与拼接问题．例如：图2中，△ABC是锐角三角形且AC＞AB，点E为AC中点，F为BC上一点且BF≠FC（F不与B、C重合），沿EF将其剪开，得到的两块图形恰能拼成一个梯形．

    请分别按下列要求用直线将图2中的△ABC重新进行分割，画出分割线及拼接后的图形．

     1.（1）在图3中将△ABC沿分割线剪开，使得到的两块图形恰能拼成一个平行四边形；

    2.（2在图4中将△ABC沿分割线剪开，使得到的三块图形恰能拼成一个矩形，且其中的两块为直角三角形；

    3.（3在图5中将△ABC沿分割线剪开，使得到的三块图形恰能拼成一个矩形，且其中的一块为锐角三角形．

     

    查看答案和解析>>

    同步练习册答案