
【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.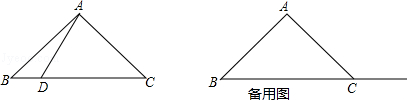
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB= ![]() ,则GE的长为
,则GE的长为 ![]() ,并简述求GE长的思路.
,并简述求GE长的思路.
【答案】
(1)
证明:①依题意补全图形,如图1所示,
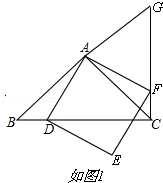
②BC⊥CG,BC=CG;
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAD+∠DAC=90°,
∠DAF=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
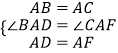
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°,
∴∠ACF+∠ACB=90°,
∴BC⊥CG;
∵点G是BA延长线上的点,
BC=CG
(2)
如图2,
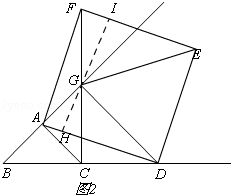
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAD﹣∠DAC=90°,
∠DAF=∠CAF﹣∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
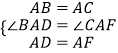
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°,BD=CF,
∴∠ACF+∠ACB=90°,
∴BC⊥CF;
∵AB= ![]() ,BC=CD=CG=GF=2,
,BC=CD=CG=GF=2,
∴在Rt△AGH中,根据勾股定理得,AG= ![]() ,
,
∴在Rt△AGH中,根据勾股定理的,DG=2 ![]() ,
,
∵AD= ![]() ,
,
∴AH= ![]() ,HG=
,HG= ![]() ,
,
∴GI=AD﹣HG= ![]() ,
,
∴GE= ![]() =
= ![]()
故答案为 ![]()
【解析】(1)①依题意补全图形,如图1所示,②判断出△BAD≌△CAF即可;(2)先判断出△BAD≌△CAF,得到BD=CF,BG⊥CF,得到直角三角形,利用勾股定理计算即可.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料3600kg,乙种原料2410kg,计划利用这两种原料生产A,B两种产品共500件,产品每月均能全部售出.已知生产一件A产品需要甲原料9kg和乙原料3kg;生产一件B种产品需甲种原料4kg和乙种原料8kg.
(1)设生产x件A种产品,写出x应满足的不等式组.
(2)问一共有几种符合要求的生产方案?并列举出来.
(3)若有两种销售定价方案,第一种定价方案可使A产品每件获得利润1.15万元,B产品每件获得利润1.25万元;第二种定价方案可使A和B产品每件都获得利润1.2万元;在上述生产方案中哪种定价方案盈利最多?(请用数据说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
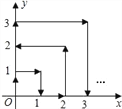
【题目】如图所示一个质点在第一象限内及x轴、y轴上运动,在第一秒内它由原点移动到(0,1)点,而后接着按图所示在x轴,y轴平行的方向运动,且每秒移动一个单位长度,那么质点运动到点(n,n)(n为正整数)的位置时,用代数式表示所用的时间为_________秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)(﹣2)﹣1﹣|﹣ ![]() |+(3.14﹣π)0+4cos45°
|+(3.14﹣π)0+4cos45°
(2)已知x2﹣2x﹣7=0,求(x﹣2)2+(x+3)(x﹣3)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
等待时间x | 1 | 2 | 5 | 10 | 20 |
舒适度指数y | 100 | 50 | 20 | 10 | 5 |
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的位置和数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,其坡度为i=1: ![]() ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)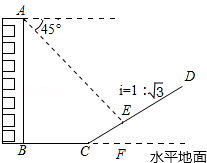
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com