
【题目】如图,已知正方形ABCD的边长为10厘米,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.设运动时间为t秒.
(1)若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,则当t为何值时,能够使△BPE与△CQP全等;此时点Q的运动速度为多少.

【答案】(1)△BPE与△CQP全等,理由见解析;(2)t=![]() ,
,
【解析】
(1)根据SAS可判定全等;
(2)由于点Q的运动速度与点P的运动速度不相等,而运动时间相同,所以BP≠CQ.又△BPE与△CQP全等,则有BP=PC=![]() BC=5,CQ=BE=6,由BP=5求出运动时间,再根据速度=路程÷时间,即可得出点Q的速度.
BC=5,CQ=BE=6,由BP=5求出运动时间,再根据速度=路程÷时间,即可得出点Q的速度.
(1)△BPE与△CQP全等.
∵点Q的运动速度与点P的运动速度相等,且t=2秒,
∴BP=CQ=2×2=4厘米,
∵AB=BC=10厘米,AE=4厘米,
∴BE=CP=6厘米,
∵四边形ABCD是正方形,
∴在Rt△BPE和Rt△CQP中,![]() ,
,
∴Rt△BPE≌Rt△CQP;
(2)∵点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C=90°,
∴要使△BPE与△OQP全等,只要BP=PC=5厘米,CQ=BE=6厘米,即可.
∴点P,Q运动的时间t=![]() (秒)
(秒)
此时点Q的运动速度为![]() (厘米/秒).
(厘米/秒).


科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是 ![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 ![]() 时,则阴影部分的面积为( )
时,则阴影部分的面积为( ) 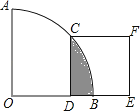
A.2π﹣4
B.4π﹣8
C.2π﹣8
D.4π﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | M | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | N |
D.不知道 | 50 | 0.25 |
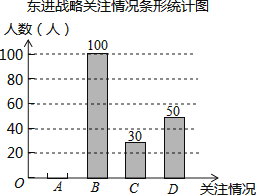
(1)根据上述统计图可得此次采访的人数为人,m= , n=
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将 ![]() 沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.
沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC. 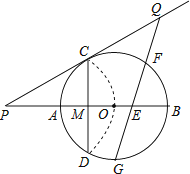
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为 ![]() 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交
的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交 ![]() 于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(5,3),点C(0,8),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC. 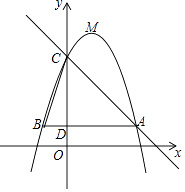
(1)求该二次函数的解析式及点M的坐标;
(2)求△ABC的面积;
(3)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E、F分别在边BC,CD上,且BE=DF,点P是AF的中点,点Q是直线AC与EF的交点,连接PQ,PD.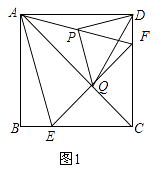
(1)求证:AC垂直平分EF;
(2)试判断△PDQ的形状,并加以证明;
(3)如图2,若将△CEF绕着点C旋转180°,其余条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.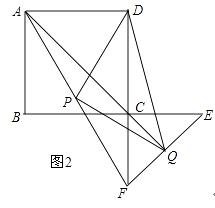
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com