【题目】如图，在正方形ABCD的外侧，作等边三角形ADE，连接BE，CE．
（1）求证：BE=CE．
（2）求∠BEC的度数
【答案】（1）证明见解析；（2）30°
【解析】
试题分析：（1）由正方形和等边三角形的性质得出AB=AE，DC=DE，∠BAE=150°，∠CDE=150°，可证ΔBAE≌ΔCDE，即可证出BE=CE；
（2）由（1）知：∠AEB=∠CED=15°，从而可求∠BEC的度数．
试题解析：（1）证明：∵四边形ABCD为正方形
∴AB=AD=CD,∠BAD=∠ ADC=90°
∵三角形ADE为正三角形
∴ AE=AD=DE,∠EAD=∠EDA=60°
∴∠BAE=∠CDE=150°
∴ΔBAE≌ΔCDE
∴BE=CE
（2）∵AB=AD, AD=AE,
∴AB=AE
∴∠ABE=∠AEB
又 ∵∠BAE=150° ∴∠ABE=∠AEB=15°
同理：∠CED=15°
∴∠BEC=600－15°×2=30°
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，AB的垂直平分线MN交AC于点D，交AB于点E．
（1）求证：△ABD是等腰三角形；
（2）若∠A=40°，求∠DBC的度数；
（3）若AE=6，△CBD的周长为20，求△ABC的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用“☆”定义一种新运算：对于任意有理数a和b，规定a☆b=ab2+2ab+a．
如：1☆3=1×32+2×1×3+1=16．
（1）求（﹣2）☆3的值；
（2）若（
☆3）☆（﹣
）=8，求a的值；
（3）若2☆x=m，（
x）☆3=n（其中x为有理数），试比较m，n的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
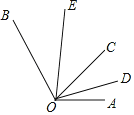
【题目】如图，∠AOB=130°，射线OC是∠AOB内部任意一条射线，OD、OE分别是∠AOC、∠BOC的角平分线，下列叙述正确的是（ ）
A. ∠DOE的度数不能确定 B. ∠AOD=
∠EOC
C. ∠AOD+∠BOE=65° D. ∠BOE=2∠COD
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明设计了一个问题,分两步完成：
(1)已知关于x的一元一次方程
,请画出数轴,并在数轴上标注a与
对应的点,分别记作A,B;
(2)在第1问的条件下,在数轴上另有一点C对应的数为y,C与A的距离是C与B的距离的5倍,且C在表示5的点的左侧,求y的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】宜宾市开展“创建全国文明城市”活动，城区某校倡议学生利用双休日在“市政广场”参加义务劳动，为了解同学们劳动情况，学校随机调查了部分同学的劳动时间，绘制了不完整的统计图，根据以下图中信息，回答下列问题：
（1）将条形统计图补充完整；
（2）填空：被调查学生劳动时间的众数是______；中位数是________；
（3）求所有被调查同学的平均劳动时间．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
