
已知一元二次方程x2-(2k+1)x+k2+k=0 .
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是这个方程的两个实数根,第三边BC的长为5.
当△ABC是等腰三角形时,求k的值.
解:(1)证明:∵一元二次方程为x2-(2k+1)x+k2+k=0,
△ =[-(2k+1)]2-4 (k2+k)=1>0, ∴此方程有两个不相等的实数根。
(2) ∵△ABC的两边AB、AC的长是这个方程的两个实数根,由(1)知,AB≠AC,△ABC第三边BC的长为5,且△ABC是等腰三角形,
∴必然有AB=5或AC=5,即x=5是原方程的一个解。
将x=5代入方程x2-(2k+1)x+k2+k=0,
25-5(2k+1) +k2 +k=0,解得k=4或k=5.
当k=4时,原方程为x2 -9x +20 = 0 ,x1=5, x2= 4, 以5,5,4为边长能构成等腰三角形;
当k=5时,原方程为x2 -11x +30 = 0 ,x1=5, x2=6, 以5,5,6为边长能构成等腰三角形;∴k的值为4或5。


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
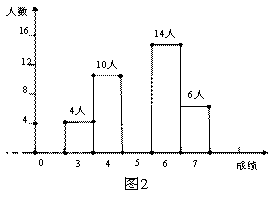 为了解某校九年级男生体育测试情况,体育老师随机抽取部分男生进行测试,并对成绩进行统计,绘制成图1和图2两幅。尚不完整的统计图
为了解某校九年级男生体育测试情况,体育老师随机抽取部分男生进行测试,并对成绩进行统计,绘制成图1和图2两幅。尚不完整的统计图
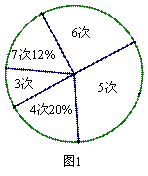 |
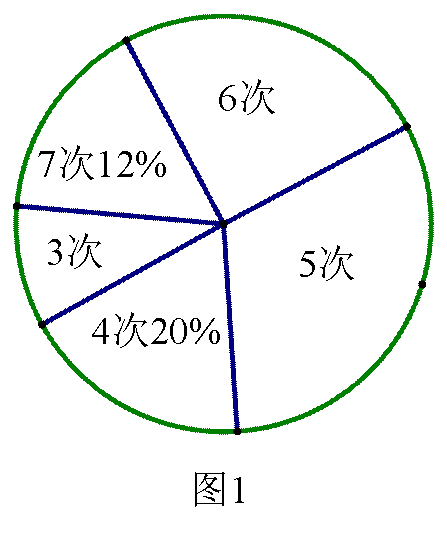
(1) 求本次抽测的男生______人。
(2) 将两幅图补充完整。
(3) 若规定引体向上5次以上(含5次)为达标,则该校350名九年级男生估计有多少人能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个布口袋内装有白、红、黑三种颜色的小球,它们除颜色之外没有任何其他区别,其中有白球5只、红球3只、黑球1只。袋中的球已经搅匀,闭上眼睛随机地从袋中取出1只球,取出红球的概率是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
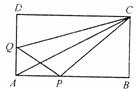
如图,在矩形ABCD中,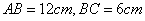 ,点P沿AB边从点A开始向点B以
,点P沿AB边从点A开始向点B以 的速度移动,点Q沿DA边从点D开始向A以
的速度移动,点Q沿DA边从点D开始向A以 的速度移动.如果P、Q同时出发,用
的速度移动.如果P、Q同时出发,用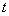 秒表示移动的时间
秒表示移动的时间 ),那么:
),那么:
(1)当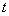 为何值时,△QPA为等腰直角三角形?
为何值时,△QPA为等腰直角三角形?
(2)对四边形QAPC的面积,提出一个与计算结果有关的结论.
(3)当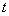 为何值时,以点Q、
为何值时,以点Q、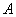 、
、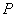 为顶点的三角形与△ABC相似?
为顶点的三角形与△ABC相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com