
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,△ADF是等腰三角形旋转角α度数为( )
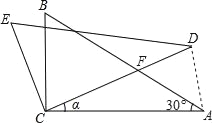
A. 20° B. 40° C. 20°或40° D. 60°
【答案】C
【解析】
根据旋转的性质可得AC=CD,根据等腰三角形的两底角相等求出∠ADF=∠DAC,再表示出∠DAF,根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠AFD,然后分①∠ADF=∠DAF,②∠ADF=∠AFD,③∠DAF=∠AFD三种情况讨论求解.
∵△ABC绕C点逆时针方向旋转得到△DEC,
∴AC=CD,
∴∠ADF=∠DAC=![]() (180°﹣α),
(180°﹣α),
∴∠DAF=∠ADC﹣∠BAC=![]() (180°﹣α)﹣30°,
(180°﹣α)﹣30°,
根据三角形的外角性质,∠AFD=∠BAC+∠DAC=30°+α,
△ADF是等腰三角形,分三种情况讨论,
①∠ADF=∠DAF时,![]() (180°﹣α)=
(180°﹣α)=![]() (180°﹣α)﹣30°,无解,
(180°﹣α)﹣30°,无解,
②∠ADF=∠AFD时,![]() (180°﹣α)=30°+α,
(180°﹣α)=30°+α,
解得α=40°,
③∠DAF=∠AFD时,![]() (180°﹣α)﹣30°=30°+α,
(180°﹣α)﹣30°=30°+α,
解得α=20°,
综上所述,旋转角α度数为20°或40°.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
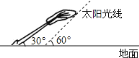
【题目】如图,太阳光线与地面成![]() 角,一棵倾斜的大树与地面成
角,一棵倾斜的大树与地面成![]() 角,这时测得大树在地面上的影长约为
角,这时测得大树在地面上的影长约为![]() ,则大树的长约为________
,则大树的长约为________![]() (保留两个有效数字,下列数据供选用:
(保留两个有效数字,下列数据供选用:![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
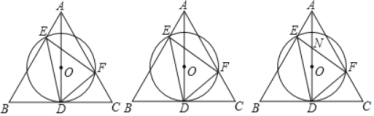
【题目】如图:AD是正△ABC的高,O是AD上一点,⊙O经过点D,分别交AB、AC于E、F
(1)求∠EDF的度数;
(2)若AD=6![]() ,求△AEF的周长;
,求△AEF的周长;
(3)设EF、AD相较于N,若AE=3,EF=7,求DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
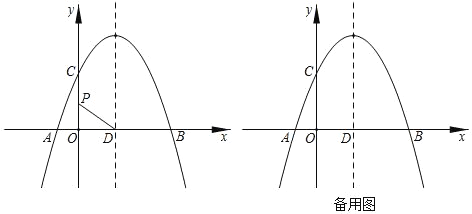
【题目】已知抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0),且与y轴交于点C,抛物线的对称轴与x轴交于点D.
(1)求抛物线的解析式;
(2)点P是y轴正半轴上的一个动点,连结DP,将线段DP绕着点D顺时针旋转90°得到线段DE,点P的对应点E恰好落在抛物线上,求出此时点P的坐标;
(3)点M(m,n)是抛物线上的一个动点,连接MD,把MD2表示成自变量n的函数,并求出MD2取得最小值时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数m、n,定义一种运算“※”为:m※n=mn+n.
(1)求2※5与2※(﹣5)的值;
(2)如果关于x的方程x※(a※x)=﹣![]() 有两个相等的实数根,求实数a的值.
有两个相等的实数根,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.
(1)试求∠DAE的度数;
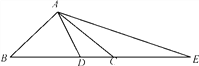
(2)如果把原题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)

查看答案和解析>>
科目:初中数学 来源: 题型:
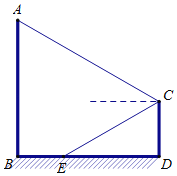
【题目】某游乐场一转角滑梯如图所示,滑梯立柱AB、CD均垂直于地面,点E在线段BD上,在C点测得点A的仰角为30°,点E的俯角也为30°,测得B、E间距离为10米,立柱AB高30米.求立柱CD的高(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com