
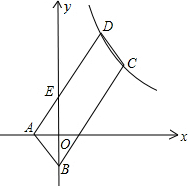
 如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-3),顶点C、D在双曲线y=$\frac{k}{x}$上,边AD交y轴于点E,且?ABCD的面积是△ABE面积的8倍,则k=36.
如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-3),顶点C、D在双曲线y=$\frac{k}{x}$上,边AD交y轴于点E,且?ABCD的面积是△ABE面积的8倍,则k=36. 分析 分别过C、D作x轴的垂线,垂足为F、G,过C点作CH⊥DG,垂足为H,根据CD∥AB,CD=AB可证△CDH≌△ABO,则CH=AO=1,DH=OB=3,由此设C(m+1,n),D(m,n+3),C、D两点在双曲线y=$\frac{k}{x}$上,则(m+1)n=m(n+3),解得n=3m,设直线AD解析式为y=ax+b,将A、D两点坐标代入求解析式,确定E点坐标,求S△ABE,根据S四边形ABCD=8S△ABE,列方程求m、n的值,根据k=(m+1)n求解.
解答 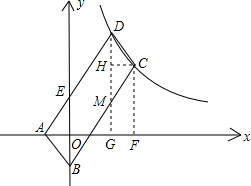 解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
∵ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=3,设C(m+1,n),D(m,n+3),
则(m+1)n=m(n+3)=k,
解得n=3m,则D的坐标是(m,3m+3),
设直线AD解析式为y=ax+b,将A、D两点坐标代入得
$\left\{\begin{array}{l}{-a+b=0①}\\{ma+b=3m+3②}\end{array}\right.$,
由①得:a=b,代入②得:mb+b=3m+3,
即b(m+1)=3(m+1),解得b=3,
则$\left\{\begin{array}{l}{a=3}\\{b=3}\end{array}\right.$,
∴y=3x+3,E(0,3),BE=6,
∴S△ABE=$\frac{1}{2}$×BE×AO=3,
∵S四边形ABCD=8S△ABE=24,
∴S四边形ABCD=2S△ABE+S四边形BEDM=24,
即6+6×m=24,
解得m=3,
∴n=3m=9,
∴k=(m+1)n=4×9=36.
故答案为:36.
点评 本题考查了反比例函数的综合运用.关键是通过作辅助线,将图形分割,寻找全等三角形,利用边的关系设双曲线上点的坐标,根据面积关系,列方程求解.


科目:初中数学 来源: 题型:解答题
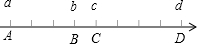 已知如图所示,数轴上A,B,C,D四个点对应的有理数是整数,若点A对应有理数a,点B对应有理数b,且b-2a=7,那么点D表示的数d是多少?
已知如图所示,数轴上A,B,C,D四个点对应的有理数是整数,若点A对应有理数a,点B对应有理数b,且b-2a=7,那么点D表示的数d是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线y=$\frac{1}{3}$x+1与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
如图,已知直线y=$\frac{1}{3}$x+1与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间t/天 | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y/千克 | 118 | 114 | 108 | 100 | 80 | 40 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
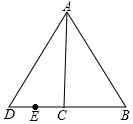 如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD.
如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
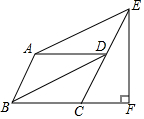 如图,在?ABCD中,∠BCD=120°,连接BD,过点A作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,若CF=2,则AB=2.
如图,在?ABCD中,∠BCD=120°,连接BD,过点A作AE∥BD交CD的延长线于点E,过点E作EF⊥BC交BC的延长线于点F,若CF=2,则AB=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | … | -0.0001 | 0 | 0.0001 | 1 | 1000 | … |
| $\root{3}{a}$ | … | -0.1 | 0 | 1 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com