
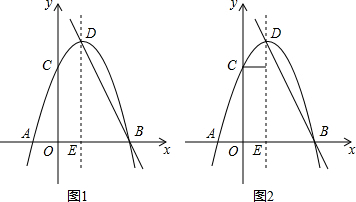
分析 (1)根据题意可得△=0且m+1≠0,解方程即可解决问题.
(2)存在.如图1中,①当P在x轴上方时,作PM⊥BD,设PM=PE=m,②当P′在x轴下方时,作P′N⊥BD于N.设P′N=P′E=m,分别构建方程即可解决问题.
(3)如图2中,当以CM为直径的⊙K与EF相切时,恰好存在两个点N,使得△MNE和△CFN相似,首先证明这个结论.设EM=a,连接KN,则KN是梯形CFEM的中位线,
可得KN=$\frac{1+a}{2}$,CM=1+a,在Rt△CMO中,根据CM2=CO2+OM2,列出方程求出a,即可解决问题.
解答 解:(1)∵一元二次方程(m+1)x2+2(m+1)x+2=0有两个相等的实数根,
∴△=0且m+1≠0,
∴4(m+1)2-4(m+1)×2=0,
解得m=±1,
∵m≠-1,
∴m=1,
∴抛物线解析式为y=-x2+2x+3.
(2)存在.如图1中,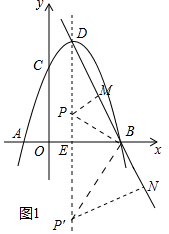
①当P在x轴上方时,作PM⊥BD,设PM=PE=m,
由题意可知A(-1,0),B(3,0),D(1,4),
,∴DE=4,BE=2,BD=$\sqrt{D{E}^{2}+E{B}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
在Rt△PDM中,∵PD2=DM2=PM2,
∴(4-m)2=(2$\sqrt{5}$-2)2+m2,
解得m=$\sqrt{5}$-1,
∴此时点P坐标(2,$\sqrt{5}$-1).
②当P′在x轴下方时,作P′N⊥BD于N.设P′N=P′E=m,
在Rt△DP′N中,∵P′D2=DN2+P′N2,
∴(4+m)2=(2$\sqrt{5}$+2)2+m2,
解得m=$\sqrt{5}$+1,
∴此时点P′坐标(2,-$\sqrt{5}$-1).
综上所述,当点P坐标为(2,$\sqrt{5}$-1)或(2,-$\sqrt{5}$-1)时,P点到x轴的距离等于P点到直线BD的距离.
(3)如图2中,当以CM为直径的⊙K与EF相切时,恰好存在两个点N,使得△MNE和△CFN相似.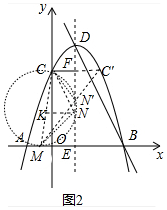
①设切点为N,则∠CNM=90°,
∵∠CFN=∠MEN=90°,
∴∠MNE+∠CNF=90°,∠CNF+∠NCF=90°,
∴∠MNE=∠NCF,
∴△MNE∽△NCF.
②作C关于直线DE的对称点C′,连接MC′交DE于N′,
∵∠CN′F=∠C′N′F=∠MN′E,∠CFN′=∠MEN′=90°,
∴△N′ME∽△N′CF.
∴当以CM为直径的⊙K与EF相切时,恰好存在两个点N,使得△MNE和△CFN相似,
设EM=a,连接KN,则KN是梯形CFEM的中位线,
∴KN=$\frac{1+a}{2}$,CM=1+a,
在Rt△CMO中,∵CM2=CO2+OM2,
∴(1+a)2=(a-1)2=32,
解得a=$\frac{9}{4}$,
∴OM=EM-OE=$\frac{9}{4}$-1=$\frac{5}{4}$,
∴点M坐标为(-$\frac{5}{4}$,0).
点评 本题考查二次函数综合题、相似三角形的判定和性质、圆的有关性质、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,学会利用参数,根据勾股定理构建方程,学会利用直径所对的圆周角是直角、解决直角三角形相似问题,属于中考压轴题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:解答题
| 售出件数 | 7 | 6 | 3 | 5 | 4 | 2 |
| 售价(元) | +3 | +2 | +1 | 0 | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
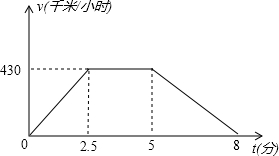 上海磁悬浮列车在一次运行中速度v(千米/小时)关于时间t(分钟)的函数图象如图,回答下列问题:
上海磁悬浮列车在一次运行中速度v(千米/小时)关于时间t(分钟)的函数图象如图,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com