

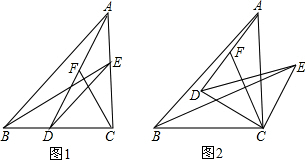
分析 (1)正三角形ABC中,可通过全等三角形来证明BM=CN,由于∠BON=∠MBC+∠BCO=60°,而∠ACB=∠ACN+∠OCB=60°,因此∠ACN=∠MBC,又知道∠A=∠BCM=60°,AC=BC,因此△ACN≌△CBM,可得出BM=CN;正方形和正五边形的证明过程与正三角形的一样,都是通过全等三角形来得出线段的相等,证三角形的过程中都是根据∠BON和多边形的内角相等得出一组两三角形中的一组对应角相等,然后根据正多边形的内角和边相等,得出BCM和CND全等,进而得出BM=CN;
(2)①由(1)的证明过程可知道∠MON的度数应该是正多边形的内角的度数,当∠BON=$\frac{(n-2)×180°}{n}$时,结论BM=CN成立,
②可参照(1)先得出三角形BCD和CDE全等,然后通过证三角形CEN和BDM全等来得出结论,在证三角形CEN和BDM全等的过程中也是通过∠BON与正五边形的内角相等得出一组对应角相等,然后根据正五边形的内角减去第一对全等三角形中得出的相等角来得出另一组对应角相等,可通过△BCD≌△CDE得出CE=BD,那么可得出三角形CEN和BDM全等,由此可得证.
解答 解:(1)选命题①
在图a中,∵△ABC是正三角形,
∴BC=CA,∠BCM=∠CAN=60°.
∵∠BON=60°,
∴∠CBM+∠BCN=60°.
∵∠BCN+∠ACN=60°,
∴∠CBM=∠ACN.
∴△BCM≌△CAN(ASA).
∴BM=CN.
选命题②
在图b中∵四边形ABCD是正方形,
∴BC=CD,∠BCM=∠CDN=90°.
∵∠BON=90°,
∴∠CBM+∠BCN=90°.
∵∠BCN+∠DCN=90°,
∴∠CBM=∠DCN.
∴△BCM≌△CDN(ASA).
∴BM=CN.
选命题③
在图c中,∵五边形ABCDE是正五边形,
∴BC=CD,∠BCM=∠CDN=108°.
∵∠BON=108°,
∴∠CBM+∠BCN=108°.
∵∠BCN+∠DCN=108°,
∴∠CBM=∠DCN.
∴△BCM≌△CDN(ASA).
∴BM=CN.
(2)①当∠BON=$\frac{(n-2)×180°}{n}$时,结论BM=CN成立.
∵在正n(n≥3)边形ABCDEF…中,
∵BC=CD,∠BCM=∠CDN=$\frac{(n-2)×180°}{n}$,
∵∠BON=$\frac{(n-2)×180°}{n}$,
∴∠CBM+∠BCN=$\frac{(n-2)×180°}{n}$,
∵∠BCN+∠DCN=$\frac{(n-2)×180°}{n}$,
∴∠CBM=∠DCN.
∴△BCM≌△CDN(ASA).
∴BM=CN.
②BM=CN成立.
在图⑤中,连接BD、CE,
∵五边形ABCDE是正五边形,
∴BC=CD,∠BCD=∠CDE=108°,CD=DE,∠CDE=∠DEA=108°.
∴∠BCD=∠DEA,
∴△BCD≌△CDE(SAS).
∴BD=CE,∠BDC=∠CED,∠DBC=∠ECD.
∵∠BON=108°,
∴∠OBC+∠OCB=108°.
∵∠OCB+∠OCD=108°,
∴∠OBC=∠OCD(即∠MBC=∠NCD).
∴∠MBC-∠DBC=∠NCD-∠ECD,即∠DBM=∠ECN.
∴∠CDE-∠BDC=∠DEA-∠CED,即∠BDM=∠CEN.
∴△BDM≌△CEN(ASA).
∴BM=CN.
点评 本题主要考查了全等三角形,正多边形等几何知识,是一道几何型探究题,层层深入,体现了一个由特殊到一般的过程,考查学生的逻辑思维能力及归纳探索诸多方面的能力,是一道很好的压轴题.本题是一道非常典型的几何探究题,很好地体现了从一般到特殊的数学思想方法,引导学生渐渐地从易走到难,是新课标形势下的成熟压轴题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
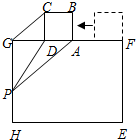 如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以lcm/s的速度沿FG方向移动,移动开始前点A与点F重合.在移动过程中,边 AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为lcm,矩形EFGH的边FG、GH的长分别为4cm、3cm.设正方形移动时间为x(s),线段GP的长为y (cm),其中0≤x≤2.5.
如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以lcm/s的速度沿FG方向移动,移动开始前点A与点F重合.在移动过程中,边 AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为lcm,矩形EFGH的边FG、GH的长分别为4cm、3cm.设正方形移动时间为x(s),线段GP的长为y (cm),其中0≤x≤2.5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一名学生骑自行车沿笔直的公路出行,这名同学离开起点的距离y(单位:千米)与行驶的时间x(单位:分)图象如图所示,则下面的结论中正确的是( )
一名学生骑自行车沿笔直的公路出行,这名同学离开起点的距离y(单位:千米)与行驶的时间x(单位:分)图象如图所示,则下面的结论中正确的是( )| A. | 整个过程的平均速度是$\frac{7}{60}$千米/时 | B. | 该同学途中停了10分钟 | ||
| C. | 前20分钟的速度比后20分钟慢 | D. | 从起点到终点共用了50分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
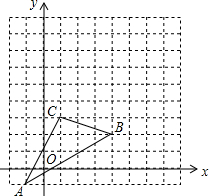 如图,三角形ABC在直角坐标系中,其中A(-1,-1).
如图,三角形ABC在直角坐标系中,其中A(-1,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com