
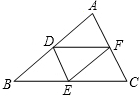
 如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,求证:△ABC∽△DEF.
如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,求证:△ABC∽△DEF.科目:初中数学 来源: 题型:
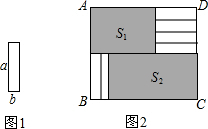 将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是( )
将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是( )A、b=
| ||
B、b=
| ||
C、b=
| ||
D、b=
|
查看答案和解析>>
科目:初中数学 来源: 题型:
2
|
|
|
|
3
|
|
4
|
|
5
|
查看答案和解析>>
科目:初中数学 来源: 题型:
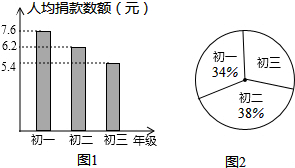 去年12月26日,印度洋发生海啸,令东南亚几国遭遇是根据我市某中学“献爱心”自愿捐款活动,学生捐款情况制成的条形统计图,图(2)是该中学学生人数比例分布(已知该校共有学生1650人).
去年12月26日,印度洋发生海啸,令东南亚几国遭遇是根据我市某中学“献爱心”自愿捐款活动,学生捐款情况制成的条形统计图,图(2)是该中学学生人数比例分布(已知该校共有学生1650人).查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2012×2013 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com