
【题目】(1)已知![]() ,求
,求![]() 的最小值.
的最小值.
爱思考的小思想到了一种方法:先用![]() 表示
表示![]() 得:
得:![]() _____;
_____;
再把![]() 代入
代入![]() 得到:
得到:![]() ______;
______;
再利用配方法得到:![]() (
(![]() _____)
_____)![]() +______;
+______;
根据完全平方式的非负性,就得到了![]() 的最小值是______.
的最小值是______.
请你补充完成小思的解答过程:
(2)根据小思的方法,请你求出:当![]() 时,求出
时,求出![]() 的最小值.
的最小值.
(3)但是假如变成![]() ,求
,求![]() 的最小值的时候小思的方法就不好用了,因此喜欢面对挑战的小喻同学想到了一种叫增量代换法:
的最小值的时候小思的方法就不好用了,因此喜欢面对挑战的小喻同学想到了一种叫增量代换法:
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
则 ,
,
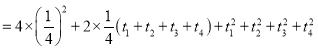 ,
,
![]() .
.
故![]() 的最小值是
的最小值是![]() .
.
参考小喻的方法,当![]() 时,
时,
求出![]() 的最小值.
的最小值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
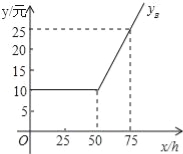
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,如果点
的中点,如果点![]() 在线段
在线段![]() 上以
上以![]() 的速度由点
的速度由点![]() 向
向![]() 点运动,同时,点
点运动,同时,点![]() 在线段
在线段![]() 上由点
上由点![]() 向
向![]() 点以
点以![]() 的速度运动.经过( )秒后,
的速度运动.经过( )秒后,![]() 与
与![]() 全等.
全等.

A.2B.3C.2或3D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠B=90°
(1)根据要求作图(尺规作图,保留作图痕迹,不写画法)
①作∠BAC的平分线AD交BC于D;
②作线段AD的垂直平分线交AB于E,交AC于F,垂足为H;
③连接ED.
(2)在(1)的基础上写出一对相似比不为1的相似三角形和一对全等三角形:
_________________________;__________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地长途汽车站规定前来乘车的旅客可以免费随身携带一定质量的行李,如果行李质量超过规定,则应交纳行李费,行李费用y(元)与行李质量x(千克)之间的关系可以用如图所示的图象表示,请观察图象回答下列问题:

(1)旅客最多能免费携带多少千克的行李?
(2)求行李费用y(元)与行李质量x(千克)之间的函数关系式;
(3)一位旅客随身携带了60千克的行李,他应交纳行李费多少元?
(4)另一位旅客交纳了120元行李费,他携带的行李重多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大刚在晚上由灯柱A走向灯柱B,当他走到M点时,发觉他身后影子的顶部刚好接触到灯柱A的底部,当他向前再走12米到N点时,发觉他身前的影子刚好接触到灯柱B的底部,已知大刚的身高是1.6米,两根灯柱的高度都是9.6米,设AM=NB=x米.求:两根灯柱之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形,

(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 | 3 | 4 | 5 | 6 | …… | n |
∠α的度数 | ______° | _____° | ______° | ______° | …… | _____° |
(2)根据规律,计算正八边形中的∠α的度数.
(3)是否存在正n边形使得∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com