
����Ŀ������ij��ѧ�������ڼ䣬��ѧУѧ�������黭��Ʒ�����꼶��������ʦ��ȫ�꼶14�����������ȡ��A��B��C��D 4���࣬������������Ʒ�����������˷���ͳ�ƣ�����������������������ͳ��ͼ�� 
��1������ʦ��ȡ�ĵ��鷽ʽ������ղ顱�������顱��������ʦ�������4������������Ʒ����������B����������Ʒ �� ���ͼ2����������
��2�����ȫ�꼶��չ��Ʒ����4�����һ�Ƚ���������2��������������2��������Ů��������Ҫ������ȥ�μ�ѧУ�ܽ������̸�ᣬ��ǡ�ó���һ��һŮ�ĸ��ʣ���Ҫ������״ͼ���б���д���������̣�
���𰸡�
��1���������飻12��3
��2���⣺����״ͼ���£�
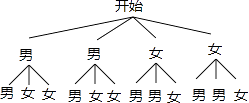
�����еȿ��ܵ������12�֣�����һ��һŮ��8�֣�
��ǡ�ó���һ��һŮ�ĸ���Ϊ�� ![]() =
= ![]() ��
��
���������⣺��1��������ʦ�������4������������Ʒ����5�� ![]() =12�������� ��B����������Ʒ��12��2��5��2=3��������
=12�������� ��B����������Ʒ��12��2��5��2=3��������
������ʦ��ȡ�ĵ��鷽ʽ�dz������飬����ʦ�������4������������Ʒ��12��������B����������Ʒ3����
�ʴ�Ϊ���������飻12��3��
��ȫͼ2����ͼ��ʾ��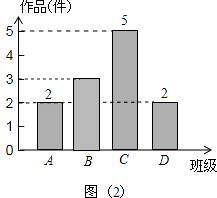
��1����������������ʦ�������4������������Ʒ����5�� ![]() =12��������B����������Ʒ��12��2��5��2=3���������̶��ɲ�ȫ����ͳ��ͼ����2�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����ǡ�ó���һ��һŮ������������ø��ʹ�ʽ������ô𰸣�
=12��������B����������Ʒ��12��2��5��2=3���������̶��ɲ�ȫ����ͳ��ͼ����2�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����ǡ�ó���һ��һŮ������������ø��ʹ�ʽ������ô𰸣�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һλͬѧ������ʵ�����������̵�һ���֣� �� ![]() ��|��1|2017�����Щ�3.14��0+4cos60��
��|��1|2017������3.14��0+4cos60��
=�� ![]() +1��1+4��
+1��1+4�� ![]() ��
��
��1��ָ������������еĴ���д����ȷ�Ľ����̣�
��2������ʽ���� ![]() +1=
+1= ![]() �Ľ��루1���е����ս����ͬ����a��ֵ��
�Ľ��루1���е����ս����ͬ����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���뾶Ϊ1�İ�Բ��ֽƬ������ͼ��ʽ�۵���ʹ���ۺ��Բ�����е�M��Բ��O�غϣ���ͼ����Ӱ���ֵ������ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Բ�Ľ�Ϊ90�������OAB�У��뾶OA=4��CΪ ![]() ���е㣬D��E�ֱ�ΪOA��OB���е㣬��ͼ����Ӱ���ֵ����Ϊ ��
���е㣬D��E�ֱ�ΪOA��OB���е㣬��ͼ����Ӱ���ֵ����Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC��Rt��DEF����ͼ��1���ڷţ���C��E�غϣ�����B��C��E����F��ͬһ��ֱ���ϣ���֪����ACB=��EDF=90�㣬��DEF=45�㣬AC=8cm��BC=6cm��EF=10cm����ͼ��2������DEF��ͼ��1����λ�ó�������1cm/s���ٶ���CB���ABC�����ƶ����ڡ�DEF�ƶ���ͬʱ����P�ӡ�ABC�Ķ���A��������2cm/s���ٶ���AB���B�����ƶ�������P�ƶ�����Bʱ����Pֹͣ�ƶ�����DEFҲ��ֹ֮ͣ�ƶ���DE��AC���ڵ�Q������PQ�����ƶ�ʱ��Ϊt��s���� 
��1���ú�t�Ĵ���ʽ��ʾ�߶�AP��AQ�ij�����д��t��ȡֵ��Χ��
��2������PE�����ı���APEQ�����Ϊy��cm2������̽��y�����ֵ��
��3����tΪ��ֵʱ����APQ�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCDEF���������Σ�����FK1K2K3K4K5K6K7���������������εĽ����ߡ������л�FK1 �� ��K1K2 �� ��K2K3 �� ��K3K4 �� ��K4K5 �� ��K5K6 �� ����Բ�����ΰ���A��B��C��D��E��Fѭ�����仡���ֱ��ΪL1 �� L2 �� L3 �� L4 �� L5 �� L6 �� ������AB=1ʱ��L2016���ڣ� �� 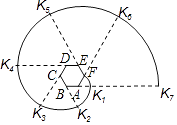
A.![]()
B.![]()
C.![]()
D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪�ı���DOBC�Ǿ��Σ���D��0��4����B��6��0����������������y= ![]() ��x��0����ͼ���߶�OC���е�A����DC�ڵ�E����BC�ڵ�F����ֱ��EF�Ľ���ʽΪy=k2x+b��
��x��0����ͼ���߶�OC���е�A����DC�ڵ�E����BC�ڵ�F����ֱ��EF�Ľ���ʽΪy=k2x+b�� 
��1������������ֱ��EF�Ľ���ʽ��
��2�����OEF�������
��3������ͼ��ֱ��д������ʽk2x+b�� ![]() ��0�Ľ⼯��
��0�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�Ϊ
A����1��1����B����3��1����C����1��4����
�ٻ�����ABC����y��ԳƵġ�A1B1C1��
�ڽ���ABC���ŵ�B˳ʱ����ת90���õ���A2BC2 �� ����ͼ�л�����A2BC2 �� ������߶�BC��ת��������ɨ�����������������У���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ��ڡ�O��AB�ǡ�O��ֱ������BAC=2��B����O������AP��OC���ӳ����ཻ�ڵ�P����PA= ![]() cm����AC�ij���
cm����AC�ij��� 
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com