
 ),C(1,
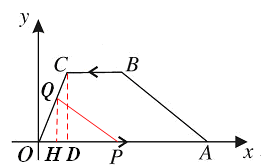
),C(1, ),动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→ C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P、Q运动的时间为t(秒).
),动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→ C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P、Q运动的时间为t(秒).
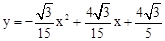 (2)
(2)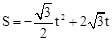 (2≤t≤3)(3)不能(4)能够交于一点,此时0≤t≤2
(2≤t≤3)(3)不能(4)能够交于一点,此时0≤t≤2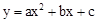 ,
,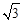 ),C(1,
),C(1,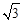 )代入得:
)代入得: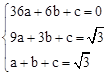 ,解得:
,解得: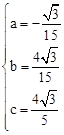 。
。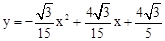 。
。
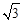 ,OC=2,
,OC=2,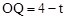 。
。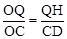 ,即
,即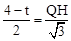 ,
, 。
。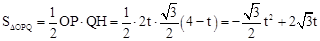 。
。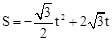 (2≤t≤3)。
(2≤t≤3)。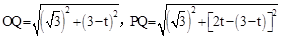 。
。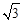 ,∴
,∴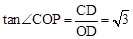 。∴
。∴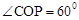 。
。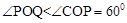 ,∴若△OPQ为直角三角形,只能是
,∴若△OPQ为直角三角形,只能是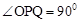 或
或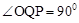 。
。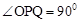 ,则
,则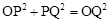 ,即
,即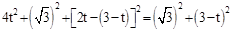 ,
, 或
或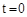 (舍去)。
(舍去)。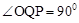 ,则
,则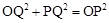 ,即
,即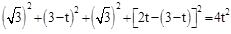 ,
,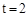 。
。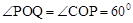 ,OQ<OC=2,
,OQ<OC=2, 或
或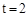 时,△OPQ为直角三角形。
时,△OPQ为直角三角形。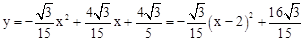 ,其对称轴为
,其对称轴为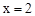 。
。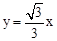 ,
,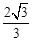 )。
)。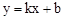 ,则
,则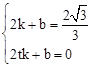 ,解得
,解得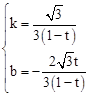 。
。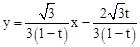 。
。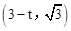 ,
,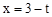 代入
代入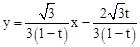 得
得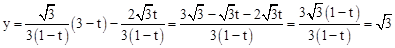 ,
,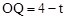 ,
,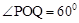 ,∴Q
,∴Q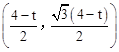 。
。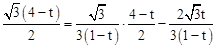 ,解得
,解得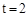 或
或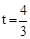 ,均不合题意,舍去。
,均不合题意,舍去。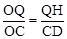 ,从而用t表示出△OPQ的边OP上的高
,从而用t表示出△OPQ的边OP上的高 ,进而根据三角形面积公式即可求得所求△OPQ的面积S与时间t的函数关系式。
,进而根据三角形面积公式即可求得所求△OPQ的面积S与时间t的函数关系式。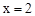 ,求出直线OB的解析式
,求出直线OB的解析式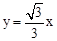 ,从而得到二者的交点
,从而得到二者的交点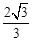 ),进而求出点P、M的直线解析式为
),进而求出点P、M的直线解析式为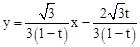 。分分点Q在BC边上运动(0≤t≤2)和点Q在CO边上运动(2<t≤3)两种情况讨论点Q与直线
。分分点Q在BC边上运动(0≤t≤2)和点Q在CO边上运动(2<t≤3)两种情况讨论点Q与直线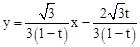 的关系,得出结论。
的关系,得出结论。

科目:初中数学 来源:不详 题型:解答题
 的图象经过点(-2,-5)、(1,4).
的图象经过点(-2,-5)、(1,4).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
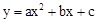 的顶点A(2,0),与y轴的交点为B(0,-1).
的顶点A(2,0),与y轴的交点为B(0,-1).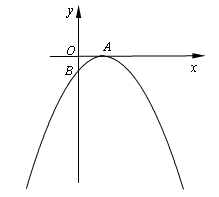
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
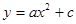 的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点
的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点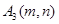 ,则
,则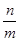 的值是 .
的值是 . 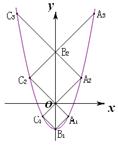
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

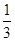 x2+bx+c经过C、D两点,求抛物线的解析式;
x2+bx+c经过C、D两点,求抛物线的解析式;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.x<2 | B.x>﹣3 | C.﹣3<x<1 | D.x<﹣3或x>1 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
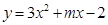 .
. 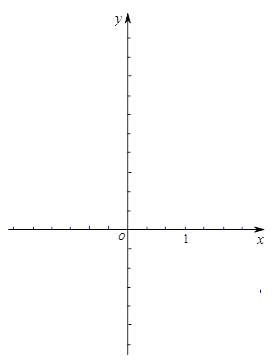
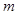 为任何实数,抛物线与x轴总有两个交点;
为任何实数,抛物线与x轴总有两个交点;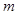 为整数,当关于x的方程
为整数,当关于x的方程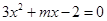 的两个有理数根都在
的两个有理数根都在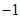 与
与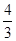 之间(不包括-1、
之间(不包括-1、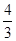 )时,求
)时,求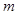 的值.
的值. 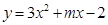 在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新图象
在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新图象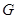 ,再将图象
,再将图象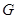 向上平移
向上平移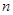 个单位,若图象
个单位,若图象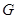 与过点(0,3)且与x轴平行的直线有4个交点,直接写出n的取值范围是 .
与过点(0,3)且与x轴平行的直线有4个交点,直接写出n的取值范围是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com