
分析 ①根据二次函数y=mx2+(5m+3)x+4m,可进行变形,得到y═(x2+5x+4)m+3x,只要令x2+5x+4=0,则所得的x的值就与m无关,从而可以解答本题;
②将m=-1代入函数解析式,然后分别令x=0和y=0求出相应的y值和x的值,即可解答本题;
③根据抛物线的解析式可以求得对称轴,然后根据m<0,可知在对称轴右侧y随x的增大而减小,然后令对称轴的值等于-$\frac{67}{26}$,求得m的值然后看m的值是否小于0,即可解答本题.
解答 解:①是真命题,
理由:∵y=mx2+(5m+3)x+4m=(x2+5x+4)m+3x,
∴当x2+5x+4=0时,得x=-4或x=-1,
∴x=-1时,y=-3;x=-4时,y=-3;
∴二次函数y=mx2+(5m+3)x+4m(m为常数且m≠0)的图象一定过定点(-1,-3),
故①是真命题;
②是假命题,
理由:当m=-1时,则函数为y=-x2-2x-4,
∵当y=0时,-x2-2x-4=0,△=(-2)2-4×(-1)×(-4)=-12<0;当x=0时,y=-4;
∴抛物线与x轴无交点,与y轴一个交点,
故②是假命题;
③是假命题,
理由:∵y=mx2+(5m+3)x+4m,
∴对称轴x=-$\frac{b}{2a}$=-$\frac{5m+3}{2m}$=-$\frac{5}{2}$-$\frac{3}{2m}$,
∵m<0,x≥-$\frac{67}{26}$时,函数y随x的增大而减小,
∴$-\frac{5}{2}-\frac{3}{2m}=-\frac{67}{26}$,得m=$\frac{39}{2}$,
∵m<0与m=$\frac{39}{2}$矛盾,
故③为假命题;
点评 本题考查二次函数的性质,解题的关键是明确题意,利用数形结合的思想解答问题.


科目:初中数学 来源: 题型:解答题
| 饮料 | 矿泉水 | 可乐 |
| 批发价(元/瓶) | 0.8 | 2.5 |
| 零售价(元/瓶) | 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | $2\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
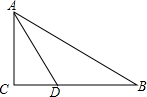 如图,在Rt△ABC中,∠C=90°,AC=4,∠A的平分线AD=$\frac{8\sqrt{3}}{3}$,求∠B的度数及边BC、AB的长.
如图,在Rt△ABC中,∠C=90°,AC=4,∠A的平分线AD=$\frac{8\sqrt{3}}{3}$,求∠B的度数及边BC、AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=20-2x(0<x<20) | B. | y=20-2x(0<x<10) | C. | y=$\frac{1}{2}$(20-x)(0<x<20) | D. | y=$\frac{1}{2}$(20-x)(0<x<10) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-9+8x=(x-3)(x+3)+8x | B. | -5x2y3=-5xy•(xy2) | ||
| C. | x2-4x-5=x(x-4-$\frac{5}{x}$) | D. | -x2+2xy=-x(x-2y) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 上网时间 | 优惠标准 |
| 0~30小时(不超过30) | 无优惠 |
| 30~50小时(不超过50) | 通讯费优惠30% |
| 50~100小时(不超过100) | 通讯费优惠40% |
| 100小时以上 | 通讯费优惠50% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com