
【题目】为了提高学生的汉字书写能力,某学校连续举办了几届汉字听写大赛,今年经过层层选拔,确定了参加决赛的选手,决赛的比赛规则是每正确听写出1个汉字得2分,满分是100分,下面是根据决赛的成绩绘制出的不完整的频数分布表、扇形统计图和频数分布直方图.
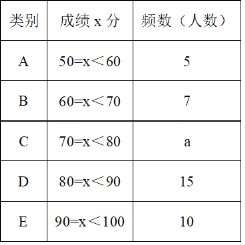
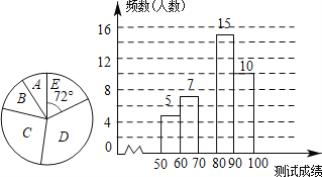
请结合图表完成下列各题
(1)表中a的值为______,并把频数分布直方图补充完整;
(2)学校想利用频数分布表估计这次决赛的平均成绩,请你直接写出平均成绩;
(3)通过与去年的决赛成绩进行比较,发现今年各类人数的中位数有了显著提高,提高了15%以上,求去年各类人数的中位数最高可能是多少?
(4)想从A类学生的3名女生和2名男生中选出两人进行培训,直接写出选中1名男生和1名女生的概率是多少.
【答案】(1)13,补全频数分布直方图见解析;(2)平均成绩为78.6;(3)去年各类人数的中位数最高可能是8;(4)选中1名男生和1名女生的概率![]() .
.
【解析】
(1)用E点的频数除以该组的频率得到调查的总人数,然后计算a的值,最后补全频数分布直方图;
(2)取组中值表示各组的平均数,然后根据加权平均数的计算方法求解;
(3)根据中位数的定义得到今年各类人数的中位数为10,然后计算10÷(1+15%)≈8.7,利用人数为整数确定去年各类人数的中位数最高;
(4)画树状图展示所有20种等可能的结果数,找出选中1名男生和1名女生的结果数,然后根据概率公式求解.
(1)调查的总人数为:10÷![]() =50,
=50,
所以![]() ;
;
故答案为:13;
频数分布直方图为:
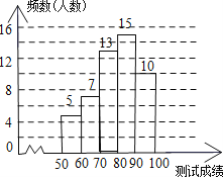
(2)平均成绩=![]() (5×55+7×65+13×75+15×85+10×95)=78.6;
(5×55+7×65+13×75+15×85+10×95)=78.6;
(3)今年各类人数的中位数为10,
10÷(1+15%)≈8.7,
而人数为整数,今年各类人数的中位数比去年提高了15%以上,
去年各类人数的中位数最高可能是:8;
(4)画树状图为:
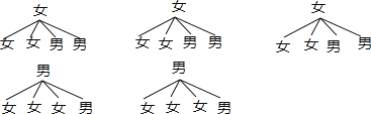
共有20种等可能的结果数,其中选中1名男生和1名女生的结果数为12,
所以选中1名男生和1名女生的概率=![]() =
=![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案科目:初中数学 来源: 题型:
【题目】问题背景:
图1,等腰△ABC中,AB=AC,∠BAC=120°,过点A作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°;于是
∠BAC=60°;于是![]() =
=![]() =
=![]() ;
;

(1)迁移应用:
如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.求证:CD=![]() AD+BD;
AD+BD;
(2)拓展延伸
如图图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.若AE=5,CE=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的顶点为A(-3,-3),此抛物线交x轴于O、 B两点.

(1)求此抛物线的解析式.
(2)求△AOB的面积 .
(3)若抛物线上另有点P满足S△POB=S△AOB,请求出P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
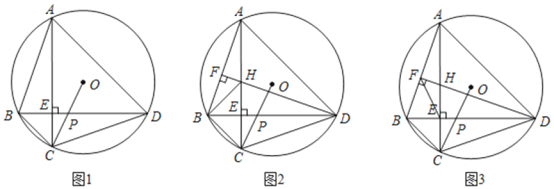
(1)如图1,求证:![]() ;
;
(2)如图2,作![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 长.
长.
查看答案和解析>>
科目:初中数学 来源: 题型:
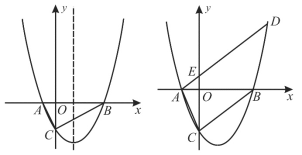
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(A点在B点的左边),与
两点(A点在B点的左边),与![]() 轴交于点
轴交于点![]() .
.
(1)如图1,若△ABC为直角三角形,求![]() 的值;
的值;
(2)如图1,在(1)的条件下,点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,若以
在抛物线的对称轴上,若以![]() 为边,以点
为边,以点![]() 、
、![]() 、
、![]() 、Q为顶点的四边形是平行四边形,求
、Q为顶点的四边形是平行四边形,求![]() 点的坐标;
点的坐标;
(3)如图2,过点![]() 作直线
作直线![]() 的平行线交抛物线于另一点
的平行线交抛物线于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() ﹕
﹕![]() =1﹕4. 求
=1﹕4. 求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+a与x轴交于点A(4,0),与y轴交于点B,抛物线y=
x+a与x轴交于点A(4,0),与y轴交于点B,抛物线y=![]() x2+bx+c经过点A,B.点M(m,0)为x轴上一动点,过点M且垂直于x轴的直线分别交直线AB及抛物线于点P,N.
x2+bx+c经过点A,B.点M(m,0)为x轴上一动点,过点M且垂直于x轴的直线分别交直线AB及抛物线于点P,N.
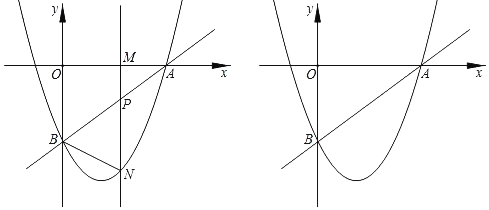
(1)填空:点B的坐标为 ,抛物线的解析式为 ;
(2)当点M在线段OA上运动时(不与点O,A重合),
①当m为何值时,线段PN最大值,并求出PN的最大值;②求出使△BPN为直角三角形时m的值;
(3)若抛物线上有且只有三个点N到直线AB的距离是h,请直接写出此时由点O,B,N,P构成的四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
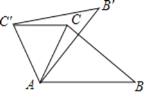
【题目】如图,在△ABC中,∠BAC=70°,将△ABC绕点A逆时针旋转,得到△AB'C',连接C'C.若C'C∥AB,则∠BAB'=______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com