
分析 (1)①根据“总利润=每辆次停车费用×辆次-总成本”列出函数解析式;
②根据“总利润=每辆次停车费用×辆次-总成本”可得函数解析式;
(2)根据停车场有3000元的日净收入,列出方程求解即可;
(3)根据(1)中函数解析式利用一次函数和二次函数性质求解可得.本题中要按照每辆次小车的停车费的变化,来分别讨论停车场的日净收入和每辆次小车的停车费之间的等量关系.然后根据不同的条件来判断出符合“使每天小车停放的辆次较多,又要有较大的日净收入”的取值.
解答 解:(1)①由题意得:y=300x-600;
②由题意得:y=[300-12(x-10)]x-600,
即y=-12x2+420x-600;
(2)依题意有:-12x2+420x-600=3000,
解得x1=15,x2=20.
故停车场能实现3000元的日净收入,每辆次轿车的停车费定价是15元或20元;
(3)当x≤10时,停车300辆次,最大日净收入y=300×10-600=2400(元)
当x>10时,
y=-12x2+420x-600
=-12(x2-35x)-600
=-12(x-17.5)2+3075
∴当x=17.5时,y有最大值.但x只能取整数,
∴x取17或18.
显然,x取17时,小车停放辆次较多,此时最大日净收入为y=-12×0.25+3075=3072(元).
由上可得,每辆次轿车的停车费定价应定为17元,此时最大日净收入是3072元.
点评 本题考查了二次函数的应用,一元二次方程的应用,根据题意列出函数关系式,再根据函数关系式解答是解题的关键.本要注意不同的条件下,函数的不同的变化,要根据题目给出的条件分别进行讨论.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
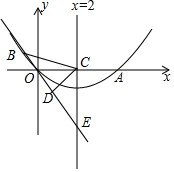 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
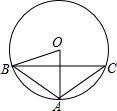 如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=4,则弦BC的长为( )
如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=4,则弦BC的长为( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
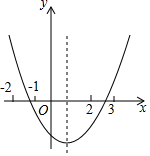 如图,图中二次函数解析式为y=ax2+bx+c(a≠0)则下列命题中正确的有①③④(填序号)
如图,图中二次函数解析式为y=ax2+bx+c(a≠0)则下列命题中正确的有①③④(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
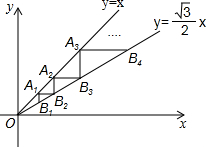 如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线y=$\frac{\sqrt{3}}{2}$x于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线y=$\frac{\sqrt{3}}{2}$x于点B3,…,按照此规律进行下去,则点An的横坐标为$(\frac{2\sqrt{3}}{3})^{n-1}$.
如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线y=$\frac{\sqrt{3}}{2}$x于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线y=$\frac{\sqrt{3}}{2}$x于点B3,…,按照此规律进行下去,则点An的横坐标为$(\frac{2\sqrt{3}}{3})^{n-1}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com