抛物线与x轴交于A(-1,0)、B两点,与y轴交于点C(0,-3),抛物线顶点为M,连接AC并延长AC交抛物线对称轴于点Q,且点Q到x轴的距离为6.
(1)求此抛物线的解析式;
(2)在抛物线上找一点D,使得DC与AC垂直,求出点D的坐标;
(3)抛物线对称轴上是否存在一点P,使得S△PAM=3S△ACM?若存在,求出P点坐标;若不存在,请说明理由.
分析:(1)设直线AC的解析式为y=kx-3,把已知坐标代入可解k的值.
(2)依题意得出∠ACO=∠ANC,然后求出ON的值以及直线CN的解析式.最后可求出x,y的值.
(3)设抛物线的对称轴交x轴于点E,依题意,得AE,EM,AM的值.设P(1,m),分情况讨论P的坐标.
解答: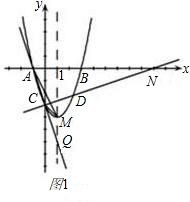
解:(1)设直线AC的解析式为y=kx-3,
把A(-1,0)代入得k=-3
∴直线AC的解析式为y=-3x-3
依题意知,点Q的纵坐标是-6
把y=-6代入y=-3x-3中,
解得x=1
∴点Q(1,-6)
∵点Q在抛物线的对称轴上
∴抛物线的对称轴为直线x=1
设抛物线的解析式为y=a(x-1)
2+n
由题意,
得
解得
∴抛物线的解析式为y=(x-1)
2-4.
(2)如图1,过点C作AC的垂线交抛物线于点
交x轴于点N,则∠ACO=∠ANC
∴tan∠ANC=tan∠ACO
∴
=∵OA=1,OC=3
∴ON=9
∴点N的坐标为(9,0)
可求得直线CN的解析式为
y=x-3由
解得
即点D的坐标为(
,
-).
(3)设抛物线的对称轴交x轴于点E,依题意,得
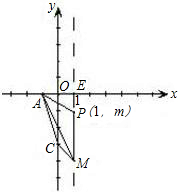
AE=2,EM=4,
AM=2∵S
△ACM=S
△AOC+S
梯形OCME-S
△AME=1
且
S△PAM=PM×AE=PM又S
△PAM=3S
△ACM∴PM=3
设P(1,m)
①当点P在点M上方时,PM=m+4=3
∴m=-1
∴P(1,-1)
②当点P在点M下方时,PM=-4-m=3
∴m=-7
∴P(1,-7)
综上所述,点P的坐标为P
1(1,-1),P
2(1,-7).
点评:本题难度较大,考查的是二次函数图象与解析式的灵活运用,一般这样题目都是作为压轴题出现,考生平时应多积累二次函数的综合知识.

 解:(1)设直线AC的解析式为y=kx-3,
解:(1)设直线AC的解析式为y=kx-3,


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案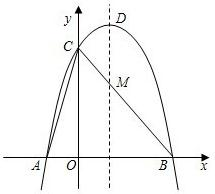 如图,已知抛物线与x轴交于A,B两点,A在B的左侧,A坐标为(-1,0)与y轴交于点C(0,3)△ABC的面积为6.
如图,已知抛物线与x轴交于A,B两点,A在B的左侧,A坐标为(-1,0)与y轴交于点C(0,3)△ABC的面积为6.
