
【题目】如图,在等边△ABC中,D、E分别是BC、AC上的点,且BD=CE,AD与BE相交于点P.下列结论:①AE=CD;②AD=BE;③∠AEB=∠ADC;④∠APE=60°.其中正确的结论共有( )
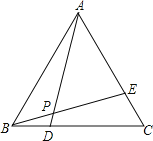
A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
先根据SAS定理得出△ABD≌△BCE,结合全等三角形的性质进行判断.
解:①∵△ABC是等边三角形,
∴AC=BC,
∵BD=CE,
∴AE=CD.故正确;

②∵△ABC是等边三角形,
∴∠ABD=∠C=60°,AB=BC.
在△ABD与△BCE中,
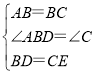 ,
,
∴△ABD≌△BCE(SAS);
∴AD=BE.
故正确;
③由②知△ABD≌△BCE,所以∠ADB=∠CEB,则∠AEB=∠ADC,故正确;
④∵由②知△ABD≌△BCE.
∴∠BAD=∠EBC,
∴∠BAD+∠ABP=∠ABD=60°.
∵∠APE是△ABP的外角,
∴∠APE=∠BAD+∠ABP=60°.
故正确.
综上所述,正确的结论有4个.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形。把它们沿图中虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为多少cm![]() ( )
( )
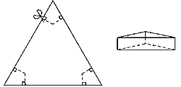
A. 124B. 144C. 110D. 94
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2014个正方形的面积为_________。
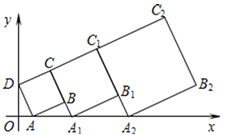
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中
中![]() 且
且![]() ,又
,又![]() 、
、![]() 为
为![]() 的三等分点.
的三等分点.

(1)求证![]() ;
;
(2)证明:![]() ;
;
(3)若点![]() 为线段
为线段![]() 上一动点,连接
上一动点,连接![]() 则使线段
则使线段![]() 的长度为整数的点的个数________.(直接写答案无需说明理由)
的长度为整数的点的个数________.(直接写答案无需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
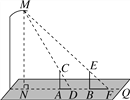
【题目】晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长(结果精确到0.01米).
查看答案和解析>>
科目:初中数学 来源: 题型:
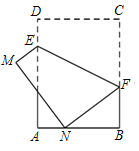
【题目】如图,在矩形ABCD中,AB=6,BC=8,点E,F分别为边AD,BC上的一个动点,连接EF,以EF为对称轴折叠四边形CDEF,得到四边形MNFE,点D,C的对应点分别为M,N,当点N恰好落在AB的三等分点时,CF的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,P为对角线BD上一动点,以P为直角顶点作Rt△PMN交直线CD于点N,交直线BC于点M,
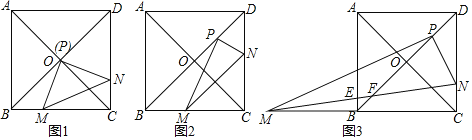
(1)如图1,若点P与对角线交点O重合时,求证:PM=PN.
(2)如图2,若点P为线段OD中点时,
①求证:BM+3DN=3;
②如图3,当M点在线段CB延长线上,且点N使得3CN=DN,MN分别交AB,BD于E,F,求线段EF的长(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCO为矩形,点A在x轴上,点C在y轴上,且点B的坐标为(-1,2),将此矩形绕点O顺时针旋转90°得矩形DEFO,抛物线y=-x2+bx+c过B,E两点.
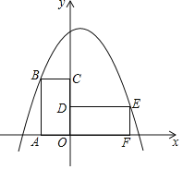
(1)求此抛物线的函数关系式;
(2)将矩形ABCO向上平移,并且使此抛物线平分线段BC,求平移距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com