
【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD关于y轴对称,边AD在x轴上,点B在第四象限,直线BD与反比例函数![]() 的图象交于点B、E.
的图象交于点B、E.
(1)求反比例函数及直线BD的解析式;
(2)求点E的坐标;
(3)连结![]() 、
、![]() 、
、![]() ,求△
,求△![]() 的面积.
的面积.

【答案】(1)反比例函数解析式: ![]() ,直线BD的解析式:
,直线BD的解析式: ![]() ;(2)E(-2,1);(3)4.
;(2)E(-2,1);(3)4.
【解析】试题分析:(1)根据正方形的边长,正方形关于y轴对称,可得点A、B、D的坐标,根据待定系数法,可得函数解析式;
(2)根据两个函数解析式,可的方程组,根据解方程组,可得答案.
(3)如图,连接EC,求出EC的解析式为y=-3x-5,再求出直线与x轴的交点P的坐标(![]() ,0),分别求出ΔEPA和ΔCPA的面积即可得解.
,0),分别求出ΔEPA和ΔCPA的面积即可得解.
试题解析:(1)边长为2的正方形ABCD关于y轴对称,边在AD在x轴上,点B在第四象限,C在第三象限,
∴A(1,0),D(-1,0),B(1,-2),C(1-,-2).
∵反比例函数y=![]() 的图象过点B,
的图象过点B,
∴![]() =-2,k=-2,
=-2,k=-2,
∴反比例函数解析式为y=-![]() ,
,
设直线BD的解析式为y=kx+b,
∴![]() ,解得
,解得![]() .
.
直线BD的解析式y=-x-1;
(2)∵直线BD与反比例函数y=![]() 的图象交于点E,
的图象交于点E,
∴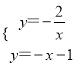 ,解得
,解得![]() 或
或![]() ,
,
∵B(1,-2),
∴E(-2,1).
(3)连接EC交x轴于点P,设EC所在的直线解析式为:y=kx+b,则有: ![]()
解得: ![]()
故EC所在直线解析式为:y=-3x-5.
当y=0时,x=-![]()
∴AP=![]()
∴SΔEAC=SΔEPA+SΔCPA=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校八年级数学兴趣小组的同学调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图。依据图中信息,解答下列问题:


(1)接受这次调查的家长共有 人;
(2)补全条形统计图;
(3)在扇形统计图中,“很赞同”的家长占被调查家长总数的百分比是 ;
(4)在扇形统计图中,“不赞同”的家长部分所对应扇形的圆心角度数是 度.
(5)请同学们对“初中生带手机上学”现象说说你的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 哥哥的身高比弟弟高是必然事件
B. 今年的12月1日有雨是不确定事件
C. 随机掷一枚均匀的硬币两次,都是正面朝上是不可能事件
D. “彩票中奖的概率为![]() ”表示买5张彩票肯定会中奖
”表示买5张彩票肯定会中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点P是∠ABC内一点.
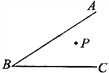
(1)画图:①过点P画BC的垂线,垂足为D;②过点P画BC的平行线交AB于点E,过点P画AB的平行线交BC于点F.
(2)∠EPF等于∠B吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发商计划将一批海产品由A地运往B地.汽车货运公司和铁路货运公司均开办海产品运输业务.已知运输路程为120千米,汽车和火车的速度分别为60千米/时、100千米/时.两货运公司的收费项目及收费标准如下表所示:
运输工具 | 运输费单价/ (元/吨·千米) | 冷藏费单价/ (元/吨·小时) | 过路费/元 | 装卸及管理费/元 |
汽 车 | 2 | 5 | 200 | 0 |
火 车 | 1.8 | 5 | 0 | 1600 |
注:“元/吨·千米”表示每吨货物每千米的运费;“元/吨·小时”表示每吨货物每小时的冷藏费.
(1)设该批发商待运的海产品有x(吨),汽车货运公司和铁路货运公司所要收取的费用分别为y1(元)和y2(元),试求y1、y2与x之间的函数关系式.
(2)若该批发商待运的海产品不少于30吨,为节省运费,他应选择哪个货运公司承担运输业务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一块长方形菜地的面积是150 m2,如果它的长减少5 m,那么菜地就变成正方形,若设原菜地的长为x m,则可列方程为___________________________________;
(2)已知如图所示的图形的面积为24,根据图中的条件,可列方程为__________________.
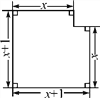
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)写出点B1的坐标;
(4)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com