
 (x-2)2+72
(x-2)2+72 ,当x=2时,S有最大值72
,当x=2时,S有最大值72 ;(3)R=2
;(3)R=2 .
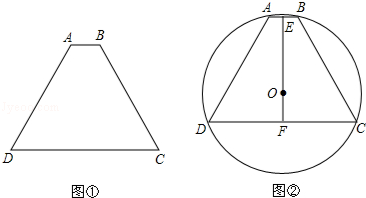
. t,然后根据等腰梯形ABCD的周长为48得3x+2t+t+3x+t+2t=48,解得t=8-x,于是可得AD=18-2x,CD=16+x;
t,然后根据等腰梯形ABCD的周长为48得3x+2t+t+3x+t+2t=48,解得t=8-x,于是可得AD=18-2x,CD=16+x; x2+8
x2+8 x+64
x+64 ,再进行配方得S=-2
,再进行配方得S=-2 (x-2)2+72
(x-2)2+72 ,然后根据二次函数的最值问题求解;
,然后根据二次函数的最值问题求解; ,所以AE=3,DF=9,由于点E和点F分别是AB和CD的中点,根据等腰梯形的性质得直线EF为等腰梯形ABCD的对称轴,所以EF垂直平分AB和CD,EF为等腰梯形ABCD的高,即EF=6
,所以AE=3,DF=9,由于点E和点F分别是AB和CD的中点,根据等腰梯形的性质得直线EF为等腰梯形ABCD的对称轴,所以EF垂直平分AB和CD,EF为等腰梯形ABCD的高,即EF=6 ,根据垂径定理的推论得等腰梯形ABCD的外接圆的圆心O在EF上,设OE=a,则OF=6
,根据垂径定理的推论得等腰梯形ABCD的外接圆的圆心O在EF上,设OE=a,则OF=6 -a,在Rt△AOE中,利用勾股定理得a2+32=R2,在Rt△ODF中,利用勾股定理得(6
-a,在Rt△AOE中,利用勾股定理得a2+32=R2,在Rt△ODF中,利用勾股定理得(6 -a)2+92=R2,然后消去R得到a的方程a2+32=(6
-a)2+92=R2,然后消去R得到a的方程a2+32=(6 -a)2+92,解得a=5
-a)2+92,解得a=5 ,最后利用R2=(5
,最后利用R2=(5 )2+32求解.
)2+32求解.
 t,
t, (AB+CD)•AH
(AB+CD)•AH (3x+16+x)•
(3x+16+x)• (8-x)
(8-x) x2+8
x2+8 x+64
x+64 ,
, (x-2)2+72
(x-2)2+72 ,
, ;
;
 ×(8-2)=6
×(8-2)=6 ,
, ,
, -a,
-a, -a)2+92=R2,
-a)2+92=R2, -a)2+92,解得a=5
-a)2+92,解得a=5 ,
, )2+32=84,
)2+32=84, .
.

科目:初中数学 来源:不详 题型:解答题
 x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:| 时间x(单位:年,x为正整数) | 1 | 2 | 3 | 4 | 5 | … |
| 单位面积租金z(单位:元/平方米) | 50 | 52 | 54 | 56 | 58 | |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,矩形
中,矩形 的边
的边 在
在 轴上,且
轴上,且 ,
, ,直线
,直线 经过点
经过点 ,交
,交 轴于点
轴于点 .
. 、
、 的坐标分别是
的坐标分别是 ( ),
( ), ( );
( ); 上且经过点
上且经过点 的抛物线的解析式;
的抛物线的解析式; 向上平移,平移后的抛物线交
向上平移,平移后的抛物线交 轴于点
轴于点 ,顶点为点
,顶点为点 .求出当
.求出当 时抛物线的解析式.
时抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com