
【题目】如图,AB为⊙O的直径,弦CD垂直平分OB于点E,点F在AB延长线上,∠AFC=30°.
(1)求证:CF为⊙O的切线.
(2)若半径ON⊥AD于点M,CE=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
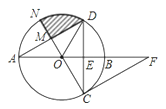
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析: (1)由CD垂直平分OB,得到E为OB的中点,且CD与OB垂直,又OB=OC,可得OE等于OC的一半,在直角三角形OEC中,根据锐角三角函数的定义,得到sin∠ECO的值为![]() ,可得∠ECO为30°,进而得到∠EOC为60°,又∠CFO为30°,可得∠OCF为直角,由OC为圆O的半径,可得CF为圆的切线,
,可得∠ECO为30°,进而得到∠EOC为60°,又∠CFO为30°,可得∠OCF为直角,由OC为圆O的半径,可得CF为圆的切线,
(2)由(1)得出的∠COF=60°,根据对称性可得∠EOD为60°,进而得到∠DOA=120°,由OA=OD,且OM与AD垂直,根据“三线合一”得到∠DOM为60°,在直角三角形OCE中,由CE的长及∠ECO=30°,可求出半径OC的长,又在直角三角形OMD中,由∠MDO=30°,半径OD=2,可求出MD及OM的长,然后利用扇形ODN的面积减去三角形ODM的面积即可求出阴影部分的面积.
试题解析:(1)证明:∵CD垂直平分OB,
∴OE=![]() OB,∠CEO=90°,
OB,∠CEO=90°,
∵OB=OC,
∴OE=![]() OC,
OC,
在Rt△COE中,sin∠ECO=![]() =
=![]() ,
,
∴∠ECO=30°,
∴∠EOC=60°,
∵∠CFO=30°,
∴∠OCF=90°,又OC是⊙O的半径,
∴CF是⊙O的切线,
(2)解:由(1)可得∠COF=60°,
由圆的轴对称性可得∠EOD=60°,∴∠DOA=120°,
∵OM⊥AD,OA=OD,∴∠DOM=60°,
在Rt△COE中,CE=![]() ,∠ECO=30°,cos∠ECO=
,∠ECO=30°,cos∠ECO=![]() ,
,
∴OC=2,
在Rt△ODM中,OD=2,∠ADO=30°,
∴OM=ODsin30°=1,MD=ODcos30°=![]() ,
,
∴S扇形OND=![]() ,
,
∴S△OMD=![]() OMDM=
OMDM=![]() ,
,
∴S阴影=S扇形OND﹣S△OMD=![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读学习:
数学中有很多恒等式可以用图形的面积来得到.
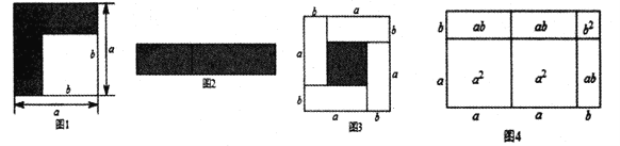
如图1,可以求出阴影部分的面积是![]() ;如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的长是a+b,宽是a-b,比较图1,图2阴影部分的面积,可以得到恒等式
;如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的长是a+b,宽是a-b,比较图1,图2阴影部分的面积,可以得到恒等式![]() .
.
(1)观察图3,请你写出![]() ,
,![]() ,
,![]() 之间的一个恒等式
之间的一个恒等式![]() _______________;
_______________;
(2)根据(1)的结论,若![]() ,
,![]() ,求出下列各式的值:①
,求出下列各式的值:①![]() ;②
;②![]() ;
;
(3)观察图4,请写出图4所表示的代数恒等式:______________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设边长为![]() 的正方形的中心
的正方形的中心![]() 在直线
在直线![]() 上,它的一组对边垂直于直线
上,它的一组对边垂直于直线![]() ,半径为
,半径为![]() 的圆的圆心
的圆的圆心![]() 在直线
在直线![]() 上运动,
上运动,![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() .
.
(![]() )如图①,当
)如图①,当![]() 时,填表:
时,填表:
| ⊙ |
|
|
|
|
| __________ |
| __________ |
| __________ |
(![]() )如图②,⊙
)如图②,⊙![]() 与正方形有
与正方形有![]() 个公共点
个公共点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,求此时
,求此时![]() 与
与![]() 之间的数量关系:
之间的数量关系:
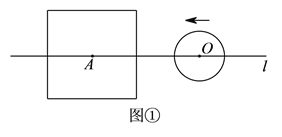

(![]() )由(
)由(![]() )可知,
)可知,![]() 、
、![]() 、
、![]() 之间的数量关系和⊙
之间的数量关系和⊙![]() 与正方形的公共点个数密切相关.当
与正方形的公共点个数密切相关.当![]() 时,请根据
时,请根据![]() 、
、![]() 、
、![]() 之间的数量关系,判断⊙
之间的数量关系,判断⊙![]() 与正方形的公共点个数.
与正方形的公共点个数.
(![]() )当
)当![]() 与
与![]() 之间满足(
之间满足(![]() )中的数量关系时,⊙
)中的数量关系时,⊙![]() 与正方形的公共点个数为__________.
与正方形的公共点个数为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,3),点C(5,c),点B的纵坐标为6且横纵坐标互为相反数,直线AC![]() 轴,直线CB
轴,直线CB![]() 轴:
轴:
(1)写出A、B、C三点坐标;
(2)求△ABC的面积;
(3)若P为线段OB上动点且点P的横、纵坐标互为相反数,当△BCP的面积大于12小于16时,求点P横坐标取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图,在△![]() 中,把
中,把![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到
得到![]() ,连接
,连接![]() ,当
,当![]() 时,我们称△
时,我们称△![]() 是△
是△![]() 的“旋补三角形”,△
的“旋补三角形”,△![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”,点
的“旋补中线”,点![]() 叫做“旋补中心”.
叫做“旋补中心”.
⑴ 特例感知:在如图、如图中,![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 是
是![]() 的“旋补中线”.
的“旋补中线”.
① 如图,当![]() 为等边三角形时,
为等边三角形时,![]() 与
与![]() 的数量关系为
的数量关系为![]() =
= ![]() ;
;
② 如图,当![]() ,
,![]() 时,则
时,则![]() 长为 .
长为 .
⑵ 精确作图:如图,已知在四边形![]() 内部存在点
内部存在点![]() ,使得
,使得![]() 是
是![]() 的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点
的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点![]() (要求:保留作图痕迹,不写作法和证明)
(要求:保留作图痕迹,不写作法和证明)
⑶ 猜想论证:在如图中,当△![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,点B在直线MN上,点A为直线PQ上一动点,连接AB.在直线AB的上方做
,点B在直线MN上,点A为直线PQ上一动点,连接AB.在直线AB的上方做![]() ,使
,使![]() ,设
,设![]() ,
,![]() 的平分线所在直线交PQ于点D.
的平分线所在直线交PQ于点D.
(1)如图1,若![]() ,且点C恰好落在直线MN上,则
,且点C恰好落在直线MN上,则![]() ________;
________;
(2)如图2,若![]() ,且点C在直线MN右侧,求
,且点C在直线MN右侧,求![]() 的度数;
的度数;
(3)若点C在直线MN的左侧,求![]() 的度数.(用含有α的式子表示)
的度数.(用含有α的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各多少万元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元. 则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=15cm,点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动;点Q从点B出发,先向点A方向运动,当与点P重合后立即改变方向与点P同向而行且速度始终为每秒2cm,设运动时间为t秒.
(1)若点P点Q同时出发,且当点P与点Q重合时,求t的值.
(2)若点P点Q同时出发,在P与Q相遇前,若点P是线段AQ的三等分点时,求t的值.
(3)若点P点Q同时出发,Q点与P点相遇后仍然继续往A点的方向运动到A点后再返回,求整个运动过程中PQ为6cm时t的值 .
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com