|
|
|
小明、小华在一栋电梯楼前感慨楼房真高.小明说:“这楼起码20层!”小华却不以为然:“20层?我看没有,数数就知道了!”小明说:“有本事,你不用数也能明白!”小华想了想说:“没问题!让我们来量一量吧!”小明、小华在楼体两侧各选A、B两点,测量数据如图,其中矩形CDEF表示楼体,AB=150米,CD=10米,∠A=30°,∠B=45°,(A、C、D、B四点在同一直线上)问:
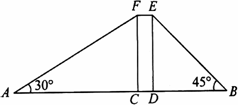
(1)楼高多少米?
(2)若每层楼按3米计算,你认为小明和小华的观点谁的正确?请说明理由.(参考数据: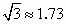 , , , ,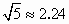 ) )
|
|
|
答案:
解析:
|
解:(1)设楼高为x米,则CF=DE=x米,
∵∠A=30°,∠B=45°,∠ACF=∠BDE=90°,
∴解得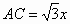 米,BD=x米, 米,BD=x米,
∴ , ,
解得 (米), (米),
∴楼高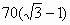 米. 米.
(2)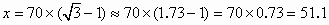 米<3×20=60米, 米<3×20=60米,
∴小华的观点正确,这楼不到20层.
|
练习册系列答案
相关习题
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
当x为何值时,下列各式在实数范围内有意义?
(1) ; ;
(2) ; ;
(3) . .
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
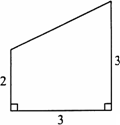
如图,在一张直角三角形纸片中,分别沿两直角边上一点与斜边中点的连线剪去两个三角形,得到如图所示的直角梯形,则原直角三角形纸片的斜边长是________.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
有四根木棒,长度分别为3,4,5,6,若取其中三根木棒组成三角形,有________种取法,其中,能构成直角三角形的是________.
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
观察下列各式,你有什么发现?
32=4+5,52=12+13,72=24+25,92=40+41,….
这到底是巧合,还是有什么规律蕴涵其中呢?请你结合有关知识进行研究.如果132=b+c,则b、c的值可能是多少?
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
在同一平面上把三边BC=3,AC=4,AB=5的三角形沿最长边AB翻折后得到△AB ,则C ,则C 的长等于 的长等于
|
| [ ] |
A. |
6
|
B. |
8
|
C. |
4.8
|
D. |
2.4
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
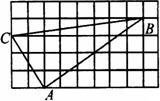
如图,若小方格边长为1,则△ABC是
|
| [ ] |
A. |
直角三角形
|
B. |
锐角三角形
|
C. |
钝角三角形
|
D. |
以上答案都不对
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
在□ABCD中,两条对角线相交于点O,点E,F,G,H分别是是OA,OB,OC,OD的中点,以图1和图2中的任意四点(即点A,B,C,D,E,F,G,H,O中的任意四点)为顶点画两种不同的平行四边形.
第一种:
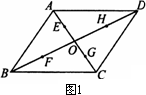
第二种:
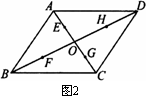
|
|
|
查看答案和解析>>
科目:初中数学
来源:新人教版(2012) 八年级下
题型:
|
|
|
如图,四边形ABCD是菱形,对角线AC、BD相交于点O.DH⊥AB于点H,连接OH.求证:∠DHO=∠DCO.
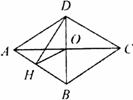
|
|
|
查看答案和解析>>
