
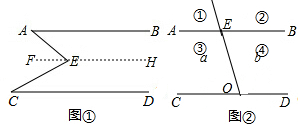
 (1)如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,EC.探究∠AEC,∠EAB,∠ECD之间的关系.
(1)如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,EC.探究∠AEC,∠EAB,∠ECD之间的关系.分析 (1)过点E画FH∥AB,根据平行线的性质,即可得到∠EAB=∠AEF,∠ECD=∠CEF,根据∠AEC=∠AEF+∠CEF,即可得到∠AEC=∠EAB+∠ECD;
(2)根据点P在①②③④4个区域,分别画出图形,依据平行线的性质以及三角形外角性质,即可得到PEB,∠POD,∠EPO之间的关系.
解答 解:(1)过点E画FH∥AB,∴∠EAB=∠AEF(两直线平行,内错角相等),
∵AB∥CD(已知),
FH∥AB(作图).
∴FH∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
∴∠ECD=∠CEF(两直线平行,内错角相等),
∵∠AEC=∠AEF+∠CEF,
∴∠AEC=∠EAB+∠ECD(等式的性质),
故答案为:两直线平行,内错角相等; 如果两条直线都与第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;∠EAB,∠ECD;
(2)如图,点P在区域①时,∠EPO=∠PEB-∠POD;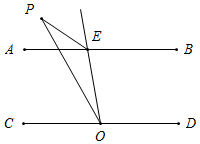
如图,点P在区域②时,∠EPO=∠POD-∠PEB; 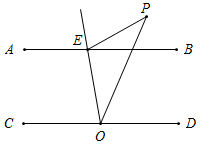
如图,点P在区域③时,∠EPO=360°-(∠PEB+∠POD); 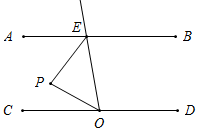
如图,点P在区域④时,∠EPO=∠PEB+∠POD.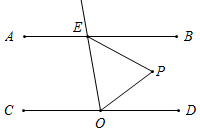
点评 本题主要考查了平行线的性质与判定,解决问题的关键是作辅助线构造内错角,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
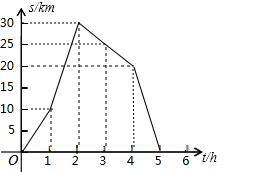 如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系.
如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com