
【题目】如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为![]() , Rt△BFC的面积为
, Rt△BFC的面积为![]() , Rt△DCE的面积为
, Rt△DCE的面积为![]() , 则
, 则![]() _______
_______ ![]() (用“>”、“=”、“<”填空);
(用“>”、“=”、“<”填空);
(2)写出图中的三对相似三角形,并选择其中一对进行证明.

科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,E是AD上任意一点,延长BA到F,使得AF=AE,连接DF:
(1)旋转△ADF可得到哪个三角形?
(2)旋转中心是哪一点?旋转了多少度?
(3)BE与DF的数量关系、位置关系如何?为什么?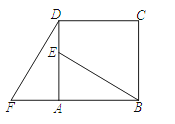
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( ) 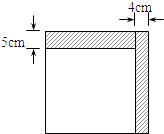
A.16cm2
B.20cm2
C.80cm2
D.160cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( ) 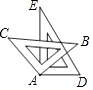
A.∠BAD≠∠EAC
B.∠DAC﹣∠BAE=45°
C.∠BAE+∠DAC=180°
D.∠DAC>∠BAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有五张正面分别标有数字﹣2,﹣1,0,1,2的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2﹣(a2+1)x﹣a+2的图象不经过点(1,0)的概率是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅.经过测试:同时开放1个大餐厅、2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅、1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅、1个小餐厅分别可供多少名学生就餐;
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com