
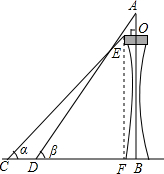
 如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7) 分析 在直角△ABD中,利用三角函数求得BD的长,则CF的长即可求得,然后在直角△CEF中,利用三角函数求得EF的长.
解答 解:在直角△ABD中,BD=$\frac{AB}{tanβ}$=$\frac{123}{tan60°}$=41$\sqrt{3}$(米),
则DF=BD-OE=41$\sqrt{3}$-10(米),
CF=DF+CD=41$\sqrt{3}$-10+40=41$\sqrt{3}$+30(米),
则在直角△CEF中,EF=CF•tanα=41$\sqrt{3}$+30≈41×1.7+30=99.7≈100(米).
答:点E离地面的高度EF是100米.
点评 本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | x2=2 | B. | x2-(k+1)x+(k+1)=0 | C. | 2x2-$\sqrt{2}$x+1=0 | D. | 1+$\frac{x}{x-1}$=$\frac{1}{x-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
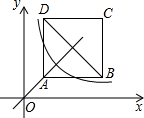 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为( )
如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为( )| A. | 1<k<9 | B. | 2≤k≤34 | C. | 1≤k≤16 | D. | 4≤k<16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
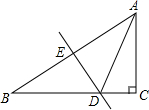 如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )
如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )| A. | 6 | B. | 6$\sqrt{3}$ | C. | 9 | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
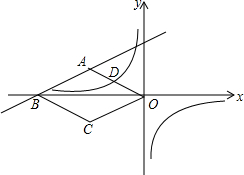 如图,在平面直角坐标系中,四边形ABCO是菱形,B、O在x轴负半轴上,AO=$\sqrt{5}$,tan∠AOB=$\frac{1}{2}$,一次函数y=k1x+b的图象过A、B两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象过OA的中点D.
如图,在平面直角坐标系中,四边形ABCO是菱形,B、O在x轴负半轴上,AO=$\sqrt{5}$,tan∠AOB=$\frac{1}{2}$,一次函数y=k1x+b的图象过A、B两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象过OA的中点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
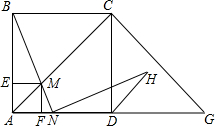 如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长AG于N.
如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长AG于N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 转化思想 | B. | 函数思想 | C. | 数形结合思想 | D. | 公理化思想 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com