
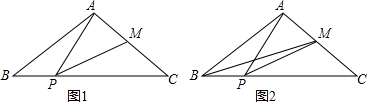
 如图,在△ABC中,己知AB=AC=10,BC=16,点p在线段BC上运动(P不与B,C重合),连接AP,做∠APM=∠B,PM交AC于点M.
如图,在△ABC中,己知AB=AC=10,BC=16,点p在线段BC上运动(P不与B,C重合),连接AP,做∠APM=∠B,PM交AC于点M.分析 (1)根据三角形的外角的性质求出∠PAB=∠MPC,根据相似三角形的判定定理证明即可;
(2)根据平行线的性质和相似三角形的性质列出比例式,得到关于x的一元二次方程,解方程即可;
(3)作AH⊥BC于H,根据勾股定理和三角形的面积公式求出△ABC的面积,根据相似三角形的性质用x表示出AM,计算即可.
解答 (1)证明:∵∠APC=∠B+∠PAB,∠APM=∠B,
∴∠PAB=∠MPC,
∵AB=AC,
∴∠B=∠C,
∴△ABP∽△PCM;
(2)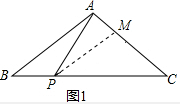 ∵PM∥AB,
∵PM∥AB,
∴∠APM=∠BAP,又∠APM=∠B,
∴∠B=∠PAB,
设BP=x,PM=y,则PC=16-x,PA=x,
∵PM∥AB,
∴$\frac{PM}{AB}$=$\frac{CP}{CB}$,即$\frac{y}{10}$=$\frac{16-x}{16}$,
整理得,5x+8y=80,①
∵△ABP∽△PCM,
∴$\frac{AB}{PC}$=$\frac{BP}{CM}$,即$\frac{10}{16-x}$=$\frac{x}{y}$,
整理得,10y=16x-x2,②
x1=16(舍去),x2=$\frac{25}{4}$,
答:PM∥AB时,线段BP的长为$\frac{25}{4}$;
(3)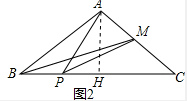 作AH⊥BC于H,
作AH⊥BC于H,
∵AB=AC=10,BC=16,
∴BH=HC=8,
由勾股定理得,AH=6,
∴△ABC的面积为:$\frac{1}{2}$×BC×AH=48,
设BP=x,
∵△ABP∽△PCM,
∴$\frac{BP}{MC}$=$\frac{AB}{PC}$,
MC=$\frac{16x-{x}^{2}}{10}$,
则AM=10-MC=$\frac{100-16x+{x}^{2}}{10}$,
∵$\frac{{S}_{△ABM}}{{S}_{△ABC}}$=$\frac{AM}{AC}$,
∴$\frac{S}{48}$=$\frac{100-16x+{x}^{2}}{100}$,
则S=$\frac{12}{25}$(x2-16x+100)=$\frac{12}{25}$(x-8)2+$\frac{432}{25}$,
∴S存在最小值是$\frac{432}{25}$.
点评 本题考查的是相似三角形的判定和性质、平行线的性质、一元二次方程的解法以及二次函数的性质,掌握相似三角形的判定定理和性质定理、理解二次函数的最值的求法是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
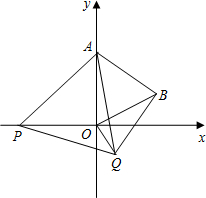 在平面直角坐标系中如图,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其右侧作等边三角形APQ,当点P运动到原点O处时,记Q的位置为B,已知在直角三角形中两直角边的平方和等于斜边的平方,即直角三角形两直角边长为a,b,斜边长为c,则a2+b2=c2.
在平面直角坐标系中如图,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其右侧作等边三角形APQ,当点P运动到原点O处时,记Q的位置为B,已知在直角三角形中两直角边的平方和等于斜边的平方,即直角三角形两直角边长为a,b,斜边长为c,则a2+b2=c2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com