
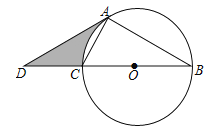
【题目】如图,以![]() 的边BC为直径作⊙O,点A在⊙O上,点D在线段BC的延长线上,AD=AB,
的边BC为直径作⊙O,点A在⊙O上,点D在线段BC的延长线上,AD=AB,![]() ,若
,若![]() 的长为
的长为![]() ,则图中阴影部分的面积__________.
,则图中阴影部分的面积__________.
【答案】![]()
【解析】
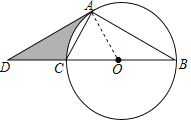
连接OA,如图,则∠COA=2∠B,由AD=AB可得∠B=∠D,进而可利用三角形的内角和得出∠OAD=90°,由弧长公式可求出半径OA的长,从而可在Rt△OAD中,利用解直角三角形的知识求出AD的长,然后根据S阴影=S△OAD﹣S扇形COA计算即可.
解:连接OA,如图,则∠COA=2∠B,
∵AD=AB,∴∠B=∠D=30°,
∴∠COA=60°,
∴∠OAD=180°﹣60°﹣30°=90°,
∵![]() 的长为
的长为![]() ,
,
∴![]() ,∴OA=2,
,∴OA=2,
在Rt△OAD中,OA=2,∠D=30°,
∴OD=2OA=4,AD=2![]() ,
,
∴S△OAD=![]() OAAD=
OAAD=![]() ×2×2
×2×2![]() =2
=2![]() ,
,
∵∠COA=60°,
∴S扇形COA=![]() ,
,
所以S阴影=S△OAD﹣S扇形COA=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像与x轴相交于点A和点B(点A在点B的左侧),与y轴相交于点C.一次函数
的图像与x轴相交于点A和点B(点A在点B的左侧),与y轴相交于点C.一次函数![]() 的图像与y轴相交于点D,其中
的图像与y轴相交于点D,其中![]() .
.
(1)分别求出A、B、C三点的坐标(可以用含有字母a的代数式表示).
(2)点P与点C关于抛物线的对称轴成轴对称,点Q为抛物线上的一个动点.
①试说明点P在直线![]() 的图像上.
的图像上.
②若点Q在抛物线上有且只有三个位置满足![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中记载:“今有上禾三秉,益实六斗,当下禾十秉.下禾五秉,益实一斗,当上禾二秉.问上、下禾实一秉各几何?”其大意是:今有上等稻子三捆,若打出来的谷子再加六斗,则相当于十捆下等稻子打出来的谷子.有下等稻子五捆,若打出来的谷子再加一斗,则相当于两捆上等稻子打岀来的谷子.问上等、下等稻子每捆能打多少斗谷子?设上等稻子每捆能打x斗谷子,下等稻子每捆能打y斗谷子,根据题意,可列方程组为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC和正方形DEFG按如图所示摆放,其中 D,E两点分别在AB,BC上,且BD=DE.若AB=12,DE=4,则△EFC的面积为( )
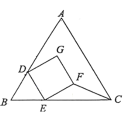
A.4B.8C.12D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
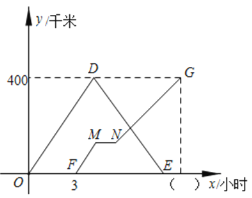
【题目】甲车从A地出发匀速驶向B地,到达B地后,立即按原路原速返回A地;乙车从B地出发沿相同路线匀速驶向A地,出发t(t>0)小时后,乙车因故在途中停车1小时,然后继续按原速驶向A地,乙车在行驶过程中的速度是80千米/时,甲车比乙车早1小时到达A地,两车距各自出发地的路程y千米与甲车行驶时间x小时之间的函数关系如图所示,请结合图象信息,解答下列问题:
(1)写出甲车行驶的速度,并直接在图中的( )内填上正确的数;
(2)求甲车从B地返回A地的过程中,y与x的函数解析式(不需要写出自变量x的取值范围);
(3)若从乙车出发至甲车到达A地,两车恰好有两次相距80千米,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题提出):有同样大小正方形256个,拼成如图1所示的![]() 的一个大的正方形.请问如果用一条直线穿过这个大正方形的话,最多可以穿过多少个小正方形?
的一个大的正方形.请问如果用一条直线穿过这个大正方形的话,最多可以穿过多少个小正方形?

(问题探究):我们先考虑以下简单的情况:一条直线穿越一个正方形的情况.(如图2)
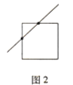
从图中我们可以看出,当一条直线穿过一个小正方形时,这条直线最多与正方形上、下、左、右四条边中的两个边相交,所以当一条直线穿过一个小正方形时,这条直线会与其中某两条边产生两个交点,并且以两个交点为顶点的线段会全部落在小正方形内.
这就启发我们:为了求出直线![]() 最多穿过多少个小正方形,我们可以转而去考虑当直线
最多穿过多少个小正方形,我们可以转而去考虑当直线![]() 穿越由小正方形拼成的大正方形时最多会产生多少个交点.然后由交点数去确定有多少根小线段,进而通过线段的根数确定下正方形的个数.
穿越由小正方形拼成的大正方形时最多会产生多少个交点.然后由交点数去确定有多少根小线段,进而通过线段的根数确定下正方形的个数.
再让我们来考虑![]() 正方形的情况(如图3):
正方形的情况(如图3):
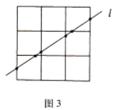
为了让直线穿越更多的小正方形,我们不妨假设直线![]() 右上方至左下方穿过一个
右上方至左下方穿过一个![]() 的正方形,我们从两个方向来分析直线
的正方形,我们从两个方向来分析直线![]() 穿过
穿过![]() 正方形的情况:从上下来看,这条直线由下至上最多可穿过上下平行的两条线段;从左右来看,这条直线最多可穿过左右平行的四条线段;这样直线
正方形的情况:从上下来看,这条直线由下至上最多可穿过上下平行的两条线段;从左右来看,这条直线最多可穿过左右平行的四条线段;这样直线![]() 最多可穿过
最多可穿过![]() 的大正方形中的六条线段,从而直线
的大正方形中的六条线段,从而直线![]() 上会产生6个交点,这6个交点之间的5条线段,每条会落在一个不同的正方形内,因此直线
上会产生6个交点,这6个交点之间的5条线段,每条会落在一个不同的正方形内,因此直线![]() 最多能经过5个小正方形.
最多能经过5个小正方形.
(问题解决):
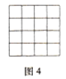
(1)有同样大小的小正方形16个,拼成如图4所示的![]() 的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过_________个小正方形.
的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过_________个小正方形.
(2)有同样大小的小正方形256个,拼成![]() 的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过___________个小正方形.
的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过___________个小正方形.
(3)如果用一条直线穿过![]() 的大正方形的话,最多可以穿过___________个小正方形.
的大正方形的话,最多可以穿过___________个小正方形.
(问题拓展):
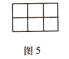
(4)如果用一条直线穿过![]() 的大长方形的话(如图5),最多可以穿过个___________小正方形.
的大长方形的话(如图5),最多可以穿过个___________小正方形.
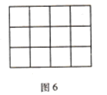
(5)如果用一条直线穿过![]() 的大长方形的话(如图6),最多可以穿过___________个小正方形.
的大长方形的话(如图6),最多可以穿过___________个小正方形.
(6)如果用一条直线穿过![]() 的大长方形的话,最多可以穿过________个小正方形.
的大长方形的话,最多可以穿过________个小正方形.
(类比探究):
由二维的平面我们可以联想到三维的立体空间,平面中的正方形中四条边可联想到正方体中的正方形的六个面,类比上面问题解决的方法解决如下问题:
(7)如图7有同样大小的小正方体8个,拼成如图所示的![]() 的一个大的正方体.如果用一条直线穿过这个大正方体的话,最多可以穿过___________个小正方体.
的一个大的正方体.如果用一条直线穿过这个大正方体的话,最多可以穿过___________个小正方体.
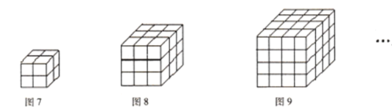
(8)如果用一条直线穿过![]() 的大正方体的话,最多可以穿过_________个小正方体.
的大正方体的话,最多可以穿过_________个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
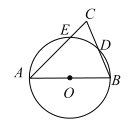
【题目】如图,AB为![]() 的直径,AC,BC分别交
的直径,AC,BC分别交![]() 于点E,D,
于点E,D,![]() ,
,![]() .现给出以下四个结论:①
.现给出以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论的序号是________.(填写所有正确结论的序号)
.其中正确结论的序号是________.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B是反比例函数y=![]() 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
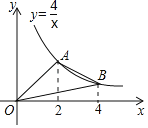
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() 的三个顶点,与
的三个顶点,与![]() 轴相交于
轴相交于![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,点
轴的对称点,点![]() 在
在![]() 轴的正半轴上.
轴的正半轴上.
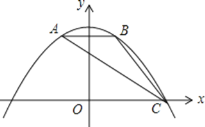
(1)求该抛物线的函数解析式;
(2)点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴,
轴,![]() 轴, 垂足分别为点
轴, 垂足分别为点![]() ,
,![]() ,当四边形
,当四边形![]() 为正方形时,求出点
为正方形时,求出点![]() 的坐标;
的坐标;
(3)将(2) 中的正方形![]() 沿
沿![]() 向右平移,记平移中的正方形
向右平移,记平移中的正方形![]() 为正方形
为正方形![]() ,当点
,当点![]() 和点
和点![]() 重合时停止运动, 设平移的距离为
重合时停止运动, 设平移的距离为![]() ,正方形的边
,正方形的边![]() 与
与![]() 交于点
交于点![]() ,
,![]() 所在的直线与
所在的直线与![]() 交于点
交于点![]() , 连接
, 连接![]() ,是否存在这样的
,是否存在这样的![]() ,使
,使![]() 是等腰三角形?若存在,求
是等腰三角形?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com