
【题目】已知二次函数y=x2+2x﹣3.
(1)求二次函数的顶点坐标;
(2)求函数与x轴交点坐标;
(3)用五点法画函数图象
x | … | … | |||||
y | … | … |
(4)当﹣3<x<0时,则y的取值范围为 .
【答案】(1)(-1,-4);(2)(﹣3,0),(1,0);(3)见解析;(4)﹣4≤y<0.
【解析】
(1)利用配方法将二次函数一般式改写为顶点式,即可得到顶点坐标;
(2)当y=0时,解一元二次方程x2+2x﹣3=0即可得出交点坐标;
(3)根据函数解析式,找出当x=-3、-2、-1、0、1时的y值,描点画图即可得;
(4)根据二次函数的性质结合函数图象,即可得出当-3<x<0时,y的取值范围.
解:(1)∵![]() ,
,
∴抛物线的顶点坐标为(-1,-4);
(2)当y=0时,x2+2x﹣3=0,解得x1=﹣3,x2=1,
∴抛物线与x轴的交点坐标为(﹣3,0)、(1,0);
(3)当x=-3时,y=x2+2x﹣3=0;
当x=-2时,y=x2+2x﹣3=-3;
当x=-1时,y=x2+2x﹣3=-4;
当x=0时,y=x2+2x﹣3=﹣3;
当x=1时,y=x2+2x﹣3=0;
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | 0 | -3 | -4 | -3 | 0 | … |
作图如下:
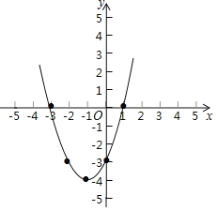
(4)由图像可知,当-3<x<0时,﹣4≤y<0.
故答案为:﹣4≤y<0.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】2019年3月21日,长春市遭遇了一次大量降雪天气,市环保系统出动了多辆清雪车连夜清雪,已知一台大型清雪车比一台小型清雪车每小时多清扫路面6千米,一台大型清雪车清扫路面90千米与一台小型清雪车清扫路面60千米所用的时间相同.求一台小型清雪车每小时清扫路面的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图,请根据图表提供的信息,解答下列问题:
分数段 (分数为x分) | 频数 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x<90 | 16 | b% |
90≤x<100 | 4 | 10% |
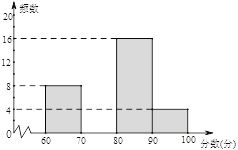
(1)表中的a= ,b= ;
(2)请补全频数分布直方图;
(3)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应的圆心角的度数是 ;
(4)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽取2名同学接受电视台记者采访,请用列表或画树状图的方法求正好抽到一名男同学和一名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学原计划加工一批校服,现有甲、乙两个工厂加工这批校服,已知甲工厂每天能加工这种校服16件,乙工厂每天加工这种校服24件,且单独加工这批校服甲厂比乙厂要多用20天
(1)求这批校服共有多少件?
(2)为了尽快完成这批校服,若先由甲、乙两工厂按原速度合作一段时间后,甲工厂停工,而乙工厂每天的速度提高25%,乙工厂单独完成剩下的部分,且乙工厂全部工作时间是甲工厂工作时间的2倍还多4天,求乙工厂加工多少天
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品现在的售价为每件60元,每星期可卖出300件. 市场调查反映:如调整价格,每降价1元,每星期可多卖出20件. 已知商品的进价为每件40元,如何定价才能使利润最大?这个最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
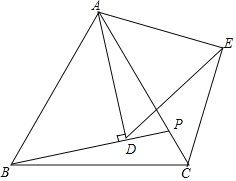
【题目】如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点;
(3)在(2)的条件下,若△ABC的边长为1,直接写出EF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
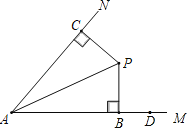
【题目】如图,点P在∠MAN内,PA平分∠MAN,PB⊥AM于点B,PC⊥AN于点C,点D是射线AM上点B右侧的一个定点.
(1)作经过A,P,D三点的圆;(保留作图痕进,不写作法)
(2)设圆与AN交于点E,∠MAN=60°,PA=4,求AE+AD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
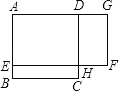
【题目】如图,ABCD是一块边长为8米的正方形苗圃,园林部门拟将其改造为矩形AEFG的形状,其中点E在AB边上,点G在A的延长线上,DG=2BE,设BE的长为x米,改造后苗圃AEFG的面积为y平方米.
(1)求y与x之间的函数关系式(不需写自变量的取值范围);
(2)若改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等,此时BE的长为 米.
(3)当x为何值时改造后的矩形苗圃AEFG的最大面积?并求出最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com