
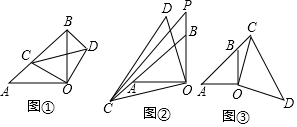
分析 (1)结论:AC=BD.只要证明△AOC≌△BOD即可解决问题.
(2)结论:CD-AB=$\sqrt{2}$AP.只要证明∠P=∠PCO,推出OP=OC,推出$\sqrt{2}$OP=$\sqrt{2}$OC,推出$\sqrt{2}$(OB+PB)=CD,推出$\sqrt{2}$OB+$\sqrt{2}$PB=CD,推出AB+$\sqrt{2}$PB=CD,即可推出CD-AB=$\sqrt{2}$PB.
(3)如图3中,①中的结论AC=BD成立.②中结论不成立.结论是:AB+CD=$\sqrt{2}$PB.证明方法类似.
解答 解:(1)结论:AC=BD.
理由:如图1中,
∵OA=OB,OC=OD,∠AOB=∠COD,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
$\left\{\begin{array}{l}{OA=OB}\\{∠AOC=∠BOD}\\{OC=OD}\end{array}\right.$,
∴△AOC≌△BOD,
∴AC=BD.
故答案为AC=BD.
(2)结论:CD-AB=$\sqrt{2}$PB.
理由:如图2中,
∵∠ABO=∠P+∠PCB,∠ABO=45°
∴∠P=45°-∠PCB,
∵∠PCO=∠DCO-∠DCP,∠DCO=45°,∠DCP=∠PCB,
∴∠PCO=45°-∠PCB,
∴∠P=∠PCO,
∴OP=OC,
∴$\sqrt{2}$OP=$\sqrt{2}$OC,
∴$\sqrt{2}$(OB+PB)=CD,
∴$\sqrt{2}$OB+$\sqrt{2}$PB=CD,
∴AB+$\sqrt{2}$PB=CD,
∴CD-AB=$\sqrt{2}$PB.
(3)如图3中,①中的结论AC=BD成立.②中结论不成立.结论是:AB+CD=$\sqrt{2}$PB.
理由:①∵OA=OB,OC=OD,∠AOB=∠COD,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
$\left\{\begin{array}{l}{OA=OB}\\{∠AOC=∠BOD}\\{OC=OD}\end{array}\right.$,
∴△AOC≌△BOD,
∴AC=BD.
②∵∠ABO=∠P+∠PCB,∠ABO=45°
∴∠P=45°-∠PCB,
∵∠PCO=∠DCO-∠DCP,∠DCO=45°,∠DCP=∠PCB,
∴∠PCO=45°-∠PCB,
∴∠P=∠PCO,
∴OP=OC,
∴$\sqrt{2}$OP=$\sqrt{2}$OC,
∴$\sqrt{2}$(PB-BO)=CD,
∴$\sqrt{2}$PB-$\sqrt{2}$BO=CD,
∴$\sqrt{2}$PB-AB=CD,
∴AB+CD=$\sqrt{2}$PB.
点评 本题考查三角形综合题、等腰直角三角形的性质、全等三角形的判定和性质、等腰三角形的判定和性质、角平分线的定义等知识,解题的关键是发现△POC是等腰三角形,题目的证明比较巧妙,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 0.1×10-8 | B. | 1×109 | C. | 0.1×108 | D. | 1×10-9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
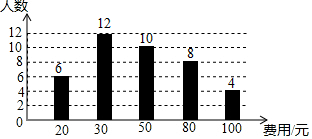 某校开展“阅读季”活动,小明调查了班级里40名同学计划购书的花费情况,并将结果绘制成如图所示的条形统计图,根据图中相关信息,这次调查获取的样本数据的众数和中位数分别是( )
某校开展“阅读季”活动,小明调查了班级里40名同学计划购书的花费情况,并将结果绘制成如图所示的条形统计图,根据图中相关信息,这次调查获取的样本数据的众数和中位数分别是( )| A. | 12和10 | B. | 30和50 | C. | 10和12 | D. | 50和30. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )| A. | ∠A=∠1+∠2 | B. | 2∠A=∠1+∠2 | C. | 3∠A=2∠1+∠2 | D. | 3∠A=2(∠1+∠2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图2×2的正方形网格放置在平面直角坐标系中,每个小正方形的顶点称为格点.每个小正方向的边长都是1,正方形ABCD的顶点都在格点上,若直线y=kx(k≠0)与正方形ABCD有公共点,则k不可能是( )
如图2×2的正方形网格放置在平面直角坐标系中,每个小正方形的顶点称为格点.每个小正方向的边长都是1,正方形ABCD的顶点都在格点上,若直线y=kx(k≠0)与正方形ABCD有公共点,则k不可能是( )| A. | 1 | B. | $\frac{1}{2}$ | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com