
【题目】如图,在平行四边形ABCD和平行四边形AECF的顶点,D,E,F,B在一条直线上,则下列等式成立的是( )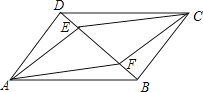
A.AE=CE
B.CE=CF
C.DE=BF
D.DE=EF=BF
【答案】C
【解析】
平行四边形的对比平行且相等,所以AB=DC,AD=BC,所以∠ABD=∠CDF,∠AEB=∠CFD,所以易证△AEB≌△CFD,故各个结论可证.
∵四边形AECF是平行四边形
∴AE=CF,CE=AF(∴A、B不成立)
∵在平行四边形AECF和平行四边形ABCD中,AE∥CF,AB∥CD
∴∠ABD=∠CDF,∠AEB=∠CFD
∵AB=CD
∴△AEB≌△CFD
∴DF=BE
∴DE=BF(∴C成立,D不成立)
故选C.
【考点精析】关于本题考查的平行四边形的性质,需要了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】某超市计划经销一些特产,经销前,围绕“A:王高虎头鸡,B:羊口咸蟹子,C:桂河芹菜,D:巨淀湖咸鸭蛋”四种特产,在全市范围内随机抽取了部分市民进行问卷调查:“我最喜欢的特产是什么?”(必选且只选一种).现将调查结果整理后,绘制成如图所示的不完整的扇形统计图和条形统计图.

(1)请补全扇形统计图和条形统计图;
(2)若全市有110万市民,估计全市最喜欢“羊口咸蟹子”的市民约有多少万人?
(3)在一个不透明的口袋中有四个分别写上四种特产标记A、B、C、D的小球(除标记外完全相同),随机摸出一个小球然后放回,混合摇匀后,再随机摸出一个小球,则两次都摸到A的概率是多少?写出分析计算过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂第一季度的电费为![]() 元,水费比电费的2倍多30元.第二季度电费比第一季度节约了30%,水费比第一季度多支出了30%.
元,水费比电费的2倍多30元.第二季度电费比第一季度节约了30%,水费比第一季度多支出了30%.
(1)该工厂第二季度水电费(电费与水费之和)为多少元?
(2)该工厂第二季度水电费与第一季度水电费相比,是增加了还是减少了?增加或减少了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年10月12日至15日,第二届中国“互联网+”大学生创新创业全国总决赛上,ofo共享单车从全国约119000个创业项目中脱颖而出,最终获得金奖. 将119000用科学计数法表示应为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知钝角△ABC,老师按照如下步骤尺规作图:
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H .
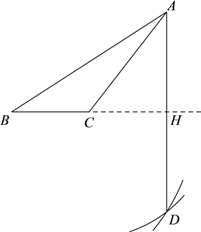
小明说:图中的BH⊥AD且平分AD.
小丽说:图中AC平分∠BAD.
小强说:图中点C为BH的中点.
他们的说法中正确的是___________.他的依据是_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读理解】
我们知道,1+2+3+…+n=![]() ,那么12+22+32+…+n2结果等于多少呢?
,那么12+22+32+…+n2结果等于多少呢?
在图1所示三角形数阵中,第1行圆圈中的数为1,即12,第2行两个圆圈中数的和为2+2,即22,…;第n行n个圆圈中数的和为![]() ,即n2,这样,该三角形数阵中共有
,即n2,这样,该三角形数阵中共有![]() 个圆圈,所有圆圈中数的和为12+22+32+…+n2.
个圆圈,所有圆圈中数的和为12+22+32+…+n2.


【规律探究】
将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n﹣1行的第一个圆圈中的数分别为n﹣1,2,n),发现每个位置上三个圆圈中数的和均为 ,由此可得,这三个三角形数阵所有圆圈中数的总和为:3(12+22+32+…+n2)= ,因此,12+22+32+…+n2= .
【解决问题】
根据以上发现,计算: ![]() 的结果为 .
的结果为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com