
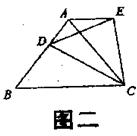
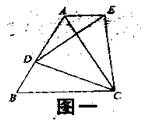
(1)如图一,等边△ABC中,D是AB上的动点,以CD为一边,向上作等边△EDC,连结AE。求证:AE//BC;
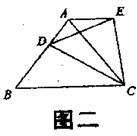
(2)如图二,将(1)中等边△ABC的形状改成以BC为底边的等腰三角形。所作△EDC改成相似于△ABC。请问:是否仍有AE//BC?证明你的结论。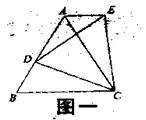
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
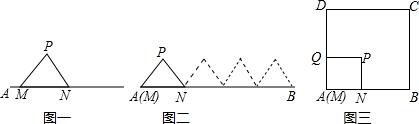
 的方向滚动, 直至△MNP中有一个点与点B重合为止,则点P经过的路程为 ;(2)如图二,正方形MNPQ的边长为1,正方形ABCD的边长为2,点M与点A重合,点N在线段AB上, 点P在正方形内部,正方形MNPQ沿正方形ABCD的边按
的方向滚动, 直至△MNP中有一个点与点B重合为止,则点P经过的路程为 ;(2)如图二,正方形MNPQ的边长为1,正方形ABCD的边长为2,点M与点A重合,点N在线段AB上, 点P在正方形内部,正方形MNPQ沿正方形ABCD的边按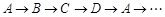 的方向滚动,始终保持M,N,P,Q四点在正方形内部或边界上,直至正方形MNPQ回到初始位置为止, 则点P经过的最短路程为 .
的方向滚动,始终保持M,N,P,Q四点在正方形内部或边界上,直至正方形MNPQ回到初始位置为止, 则点P经过的最短路程为 .
 的方向滚动指的是先以顶点N为中心
的方向滚动指的是先以顶点N为中心查看答案和解析>>
科目:初中数学 来源:2005年初中毕业升学考试(江苏苏州卷)数学(解析版) 题型:解答题
(1)如图一,等边△ABC中,D是AB上的动点,以CD为一边,向上作等边△EDC,连结AE。求证:AE//BC;
(2)如图二,将(1)中等边△ABC的形状改成以BC为底边的等腰三角形。所作△EDC改成相似于△ABC。请问:是否仍有AE//BC?证明你的结论。
查看答案和解析>>
科目:初中数学 来源:2012届浙江省台州六校九年级上学期第二次联考数学卷(解析版) 题型:填空题
(1) 如图一,等边三角形MNP的边长为1,线段AB的长为4,点M与A重合,点N在线段AB上.
△MNP沿线段AB按 的方向滚动,
直至△MNP中有一个点与点B重合为止,则点P经过的路程为
;(2)如图二,正方形MNPQ的边长为1,正方形ABCD的边长为2,点M与点A重合,点N在线段AB上, 点P在正方形内部,正方形MNPQ沿正方形ABCD的边按
的方向滚动,
直至△MNP中有一个点与点B重合为止,则点P经过的路程为
;(2)如图二,正方形MNPQ的边长为1,正方形ABCD的边长为2,点M与点A重合,点N在线段AB上, 点P在正方形内部,正方形MNPQ沿正方形ABCD的边按 的方向滚动,始终保持M,N,P,Q四点在正方形内部或边界上,直至正方形MNPQ回到初始位置为止, 则点P经过的最短路程为 .
的方向滚动,始终保持M,N,P,Q四点在正方形内部或边界上,直至正方形MNPQ回到初始位置为止, 则点P经过的最短路程为 .

(注:以△MNP为例,△MNP沿线段AB按 的方向滚动指的是先以顶点N为中心
的方向滚动指的是先以顶点N为中心
顺时针旋转,当顶点P落在线段AB上时, 再以顶点P为中心顺时针旋转,如此继续. 多边形沿直线滚动与此类似.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com