
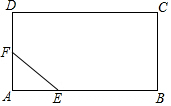
 如图,有一块矩形钢板ABCD,先截去了一个直角三角形AEF,得到一个五边形EBCDF,已知AB=200cm,BC=160cm,AE=60cm,AF=40cm,要从这块钢板上再截出一块矩形板料,如何设计才能使矩形板料的面积最大?最大面积是多少?
如图,有一块矩形钢板ABCD,先截去了一个直角三角形AEF,得到一个五边形EBCDF,已知AB=200cm,BC=160cm,AE=60cm,AF=40cm,要从这块钢板上再截出一块矩形板料,如何设计才能使矩形板料的面积最大?最大面积是多少? 分析 在EF上取一点P,过点P作QR∥AD,过点P作PO∥AB,设PO=xcm,矩形POCR的面积为ycm2,利用△PQE∽△FAE求得PQ=$\frac{2}{3}$(x-140),继而知RP=160-$\frac{2}{3}$(x-140)=$\frac{2}{3}$(380-x),根据矩形面积公式转化为二次函数的问题确定函数的最大值即可解决问题.
解答 解:如图,在EF上取一点P,过点P作QR∥AD,过点P作PO∥AB,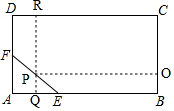
设PO=xcm,矩形POCR的面积为ycm2,
由题意知△PQE∽△FAE,
∴$\frac{PQ}{FA}$=$\frac{QE}{AE}$,即$\frac{PQ}{40}$=$\frac{x-(200-60)}{60}$,
∴PQ=$\frac{2}{3}$(x-140),
∴RP=160-$\frac{2}{3}$(x-140)=$\frac{2}{3}$(380-x),
∴y=x[$\frac{2}{3}$(380-x)]=-$\frac{2}{3}$(x-190)2+$\frac{72200}{3}$,(140≤x≤200),
∴当x=190时,最大面积为$\frac{72200}{3}$cm2,
答:在EF上取一点P,使其到BC的距离为190cm,沿点P且平行于矩形的两边截取矩形面积最大,最大面积为$\frac{72200}{3}$cm2.
点评 本题主要考查了二次函数的应用,根据实际问题选择合适的函数模型来解决实际问题,理解函数的最值及其几何意义是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | -1 | 0 | 1 |
| y | 1 | m | -1 |
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … |
| 分割成的三角形的个数 | 4 | 6 | 8 | 10 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
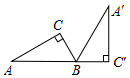 如图,Rt△A'BC'是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C'在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,则Rt△ABC旋转到Rt△A'BC'所扫过的面积为$\frac{16}{3}$π+2$\sqrt{3}$.
如图,Rt△A'BC'是由Rt△ABC绕B点顺时针旋转而得,且点A,B,C'在同一条直线上,在Rt△ABC中,若∠C=90°,BC=2,AB=4,则Rt△ABC旋转到Rt△A'BC'所扫过的面积为$\frac{16}{3}$π+2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com