
| A. | $\sqrt{3}$+$\sqrt{5}$=$\sqrt{8}$ | B. | $\sqrt{8}$-$\sqrt{3}$=$\sqrt{8-3}$ | C. | $\sqrt{3\frac{2}{3}}$=3$\sqrt{\frac{2}{3}}$ | D. | $\frac{\sqrt{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{5}$ |
分析 根据各个选项中的式子可以求得正确的结果,从而可以解答本题.
解答 解:∵$\sqrt{3}+\sqrt{5}$不能合并,故选项A错误,
∵$\sqrt{8}-\sqrt{3}=2\sqrt{2}-\sqrt{3}$,故选项B错误,
∵$\sqrt{3\frac{2}{3}}=\sqrt{\frac{11}{3}}=\frac{\sqrt{33}}{3}$,故选项C是错误的,
∵$\frac{\sqrt{2}}{\sqrt{5}}=\frac{\sqrt{10}}{5}$,故选项D是正确的,
故选D.
点评 本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
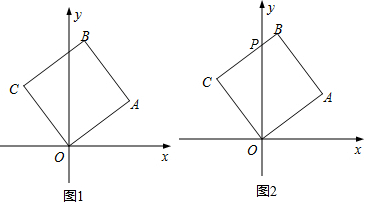
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
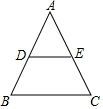 如图,在△ABC中,AB=AC,DE∥BC,则下列结论中,不正确的是( )
如图,在△ABC中,AB=AC,DE∥BC,则下列结论中,不正确的是( )| A. | AD=AE | B. | DE=$\frac{1}{2}$EC | C. | ∠ADE=∠C | D. | DB=EC |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com