
【题目】在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且∠PAC+∠PCA=![]() ,连接PB,试探究PA、PB、PC满足的等量关系.
,连接PB,试探究PA、PB、PC满足的等量关系.
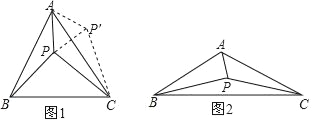
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到△ACP′,连接PP′,如图1所示.由△ABP≌△ACP′可以证得△APP′是等边三角形,再由∠PAC+∠PCA=30°可得∠APC的大小为 度,进而得到△CPP′是直角三角形,这样可以得到PA、PB、PC满足的等量关系为 ;
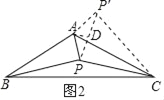
(2)如图2,当α=120°时,参考(1)中的方法,探究PA、PB、PC满足的等量关系,并给出证明;
(3)PA、PB、PC满足的等量关系为 .
【答案】(1)150,PA2+PC2=PB2;(2)3PA2+PC2=PB2;(3)4PA2sin2![]() +PC2=PB2
+PC2=PB2
【解析】试题分析:(1)根据旋转变换的性质得到△PAP′为等边三角形,得到∠P′PC=90°,根据勾股定理解答即可;
(2)如图2,作将△ABP绕点A逆时针旋转120°得到△ACP′,连接PP′,作AD⊥PP′于D,根据余弦的定义得到PP′=![]() PA,根据勾股定理解答即可;
PA,根据勾股定理解答即可;
(3)与(2)类似,根据旋转变换的性质、勾股定理和余弦、正弦的关系计算即可.
试题解析:
(1)∵△ABP≌△ACP′,
∴AP=AP′,
由旋转变换的性质可知,∠PAP′=60°,P′C=PB,
∴△PAP′为等边三角形,
∴∠APP′=60°,
∵∠PAC+∠PCA=![]() =30°,
=30°,
∴∠APC=150°,
∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∴PA2+PC2=PB2,
故答案为:150,PA2+PC2=PB2;
(2)如图2,作将△ABP绕点A逆时针旋转120°得到△ACP′,连接PP′,
作AD⊥PP′于D,
由旋转变换的性质可知,∠PAP′=120°,P′C=PB,
∴∠APP′=30°,
∵∵∠PAC+∠PCA=![]() =60°,
=60°,
∴∠APC=120°,
∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∵∠APP′=30°,
∴PD=![]() PA,
PA,
∴PP′=![]() PA,
PA,
∴3PA2+PC2=PB2;
(3)如图2,与(2)的方法类似,
作将△ABP绕点A逆时针旋转α得到△ACP′,连接PP′,
作AD⊥PP′于D,
由旋转变换的性质可知,∠PAP′=α,P′C=PB,
∴∠APP′=90°﹣![]() ,
,
∵∵∠PAC+∠PCA=![]() ,
,
∴∠APC=180°﹣![]() ,
,
∴∠P′PC=(180°﹣![]() )﹣(90°﹣
)﹣(90°﹣![]() )=90°,
)=90°,
∴PP′2+PC2=P′C2,
∵∠APP′=90°﹣![]() ,
,
∴PD=PAcos(90°﹣![]() )=PAsin
)=PAsin![]() ,
,
∴PP′=2PAsin![]() ,
,
∴4PA2sin2![]() +PC2=PB2,
+PC2=PB2,
故答案为:4PA2sin2![]() +PC2=PB2.
+PC2=PB2.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】某学校为使学生及时穿上合身的校服,现提前对该校八年级四班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为 6 个型号)

根据以上信息,解答下列问题(请写出每个空所需的求解步骤)
(1)该班共有多少名学生?其中穿 175 型号校服的学生有多少?
(2)在条形统计图中,请把空缺部分补充完整;(提醒:有两处需要补充)
(3)在扇形统计图中,185 型校服所对应的扇形圆心角的大小是 度;
(4)该班学生所穿校服型号的众数是 型,中位数是 型。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校办公楼前有一长为![]() ,宽为
,宽为![]() 的长方形空地,在中心位置留出一个半径为
的长方形空地,在中心位置留出一个半径为![]() 的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.
的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.

(1)用含字母和![]() 的式子表示阴影部分的面积;
的式子表示阴影部分的面积;
(2)当![]() =4,
=4,![]() =3,
=3,![]() =1,
=1,![]() =2时,阴影部分面积是多少?(
=2时,阴影部分面积是多少?(![]() 取3)
取3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的A、B两点所表示的数分别为a、b,a+b<0,ab<0.

(1)原点O的位置在
A.点A的右边
B.点B的左边
C.点A与点B之间 ,且靠近点A
D.点A与点B之间 ,且靠近点B
(2)若a-b=2,
①利用数轴比较大小,a 1,b -1;(填“>”、“<”或“=”).
②化简:|a-1|+|b+1|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程ax2﹣2(a﹣1)x+a﹣2=0(a>0).
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x1,x2(其中x1>x2).若y是关于a的函数,且y=ax2x1,求这个函数的表达式;
(3)将(2)中所得的函数的图象在直线a=2的左侧部分沿直线a=2翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象直接写出:当关于a的函数y=2a+b的图象与此图象有两个公共点时,b的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
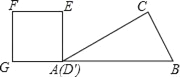
【题目】如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2![]() 为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
A. 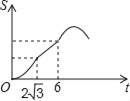 B.
B. 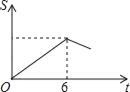 C.
C. 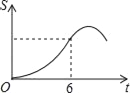 D.
D. 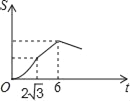
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB的两端点的坐标为A(﹣1,0),B(0,﹣2).现请你在坐标轴上找一点P,使得以P、A、B为顶点的三角形是直角三角形,则满足条件的P点的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=![]() DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com