
有四张形状、大小和质地相同的卡片A、B、C、D,正面分别写有一个正多边形(所有正多边形的边长相等),把四张卡片洗匀后正面朝下放在桌面上,从中随机抽取一张(不放回),接着再随机抽取一张.

(1)请你用画树形图或列表的方法列举出可能出现的所有结果;
(2)如果在(1)中各种结果被选中的可能性相同,求两次抽取的正多边形能构成平面镶嵌的概率;
(3)若两种正多边形构成平面镶嵌,p、q表示这两种正多边形的个数,x、y表示对应正多边形的每个内角的度数,则有方程px+qy=360,求每种平面镶嵌中p、q的值.
(1)见解析;(2)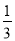 ;(3)p=3,q=2;p=4,q=1或p=2,q=2.
;(3)p=3,q=2;p=4,q=1或p=2,q=2.
【解析】
试题分析:(1)根据题意画出表格,求出所有的结果;(2)根据密铺找出符合条件的几种情况,然后计算概率;(3)本题根据密铺的性质分正方形和正三角形密铺以及正三角形和正六边形密铺两种情况进行计算.
试题解析:(1)所有出现的结果共有如下12种:
第一次/第二次 | A | B | C | D |
A | BA | CA | DA | |
B | AB | CB | DB | |
C | AC | BC | DC | |
D | AD | BD | CD |
(2)因为12种结果中能构成平面镶嵌的有4种:AB,BA,AD,DA
所以P(两次抽取的正多边形能构成平面镶嵌)=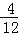 =
=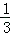 .
.
(3)当正三角形和正方形构成平面镶嵌时,则有60p+90q=360,即2p+3q=12.
因为p、q是正整数, 所以p=3,q=2,
当正三角形和六边形构成平面镶嵌时, 则有60p+120q=360,即p+2q=6.
因为p、q是正整数, 所以p=4,q=1或p=2,q=2.
考点:概率的计算、平面镶嵌问题.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源:2014-2015学年福建龙岩江山中学七年级第一学期第三次月考数学试卷(解析版) 题型:填空题
已知x=-3是关于x的方程3x -2k=1的解,则k的值是______.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省七年级上学期期末检测数学试卷(解析版) 题型:选择题
下列各组数中,互为相反数的是( ).
A.2与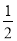 B.(- 1)2与1 C.- 1与(- 1)2 D.2与| -2|
B.(- 1)2与1 C.- 1与(- 1)2 D.2与| -2|
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级实验B班1月联考数学试卷(解析版) 题型:填空题
将一次函数 的图象先沿
的图象先沿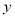 轴向上平移3个单位,再沿
轴向上平移3个单位,再沿 轴向右平移2个单位后得到的图象对应的函数关系式为 .
轴向右平移2个单位后得到的图象对应的函数关系式为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级实验B班1月联考数学试卷(解析版) 题型:选择题
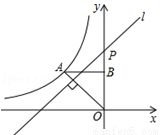
如图,反比例函数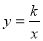 (
(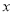 <0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,
<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,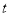 ),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则
),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则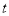 的值是( )
的值是( )
A.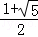 B.
B.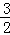 C.
C.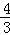 D.
D.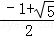
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级普通C班1月联考数学试卷(解析版) 题型:解答题
(本题8分)一只不透明的箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同.
(1)从箱子中随机摸出一个球是白球的概率是多少?
(2)从箱子中随机摸出一个球,记录下颜色后不将它放回箱子,搅匀后再摸出一个球,求两次摸出的球都是白球的概率,并画出树状图.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省郴州市九年级上学期期中考试数学试卷(解析版) 题型:选择题
在平面直角坐标系中,反比例函数y= (k<0)图像的两支分别在( )
(k<0)图像的两支分别在( )
A.第一、三象限 B.第二、四象限
C.第一、二象限 D.第三、四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com